
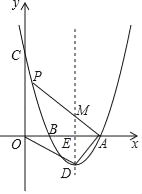
【题目】如图,抛物线y=mx2﹣8mx+12m(m>0)与x轴交于A,B两点(点B在点A的左侧),与y轴交于点C,顶点为D,其对称轴与x轴交于点E,联接AD,OD.
(1)求顶点D的坐标(用含m的式子表示);
(2)若OD⊥AD,求该抛物线的函数表达式;
(3)在(2)的条件下,设动点P在对称轴左侧该抛物线上,PA与对称轴交于点M,若△AME与△OAD相似,求点P的坐标.
【答案】(1)顶点D的坐标为(4,﹣4m);(2)y=![]() x2﹣4
x2﹣4![]() x+6
x+6![]() ;(3)点P的坐标(0,6
;(3)点P的坐标(0,6![]() )或(1,
)或(1,![]() ).
).
【解析】分析:(1)把抛物线解析式配成顶点式得到D点坐标;
(2)先解方程mx2-8mx+12m=0得到A(6,0),B(2,0),再证明△DEO∽△AED,利用相似比得到4m:2=4:4m,然后求出m即可得到抛物线解析式;
(3)由(2)得D(4,-2![]() ),利用相似的传递性得到△AME与△EAD相似,由于∠ADO=∠AEM=90°,根据相似三角形的判定,当
),利用相似的传递性得到△AME与△EAD相似,由于∠ADO=∠AEM=90°,根据相似三角形的判定,当![]() 时,△AEM∽△DEA,即
时,△AEM∽△DEA,即![]() ,解得EM=
,解得EM=![]() ,当
,当![]() ,则EM=DE=2
,则EM=DE=2![]() ,则EM=DE=2
,则EM=DE=2![]() ,分别确定对应M点的坐标,求出相应直线AM的解析式,然后把直线AM的解析式与抛物线解析式组成方程组,再解方程组可得到对应P点坐标.
,分别确定对应M点的坐标,求出相应直线AM的解析式,然后把直线AM的解析式与抛物线解析式组成方程组,再解方程组可得到对应P点坐标.
详解:(1)∵y=m(x﹣4)2﹣4m,
∴顶点D的坐标为(4,﹣4m);
(2)当y=0时,mx2﹣8mx+12m=0,解得x1=2,x2=6,
∴A(6,0),B(2,0),
∴OA=6,
∵抛物线的对称轴为x=4,
∴点E(4,0),
则OE=4,AE=2,DE=4m,
∵OD⊥AD,
∴∠ADO=90°,即∠ODE+∠ADE=90°,
而∠ODE+∠DOE=90°,
∴∠DOE=∠ADE,
∴△DEO∽△AED,
∴DE:AE=OE:DE,即4m:2=4:4m,解得m1=![]() ,m2=﹣
,m2=﹣![]() (舍去),
(舍去),
∴抛物线解析式为y=![]() x2﹣4
x2﹣4![]() x+6
x+6![]() ;
;
(3)由(2)得D(4,﹣2![]() ),
),
∵△ADO与△AED相似,△AME与△OAD相似
∴△AME与△EAD相似,
∵∠ADO=∠AEM=90°,
∴当![]() 时,△AEM∽△DEA,即
时,△AEM∽△DEA,即![]() ,解得EM=
,解得EM=![]() ,
,
∴M(4,![]() )
)
易得直线AM的解析式为y=﹣![]() x+3
x+3![]() ,
,
解方程组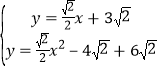 得
得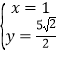 或
或![]() ,
,
∴此时P点坐标为(1,![]() ),
),
当![]() ,则EM=DE=2
,则EM=DE=2![]() ,
,
∴M(4,2![]() ),
),
易得直线AM的解析式为y=﹣![]() x+6
x+6![]() ,
,
解方程组 得
得![]() 或
或![]() ,
,
∴此时P点坐标为(0,6![]() ),
),
综上所述,点P的坐标(0,6![]() )或(1,
)或(1,![]() ).
).


科目:初中数学 来源: 题型:
【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形ABCD中E是AB的中点,P在射线DC上从D出发以每秒1个单位长度的速度运动,过P做PF⊥DE,当运动时间为__________秒时,以点P、F、E为顶点的三角形与△AED相似

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面三行数:
①-3,9,-27,81,-243,……
②-5,7,-29,79,-245,……
③- 1,3,-9,27,-81,……
(1)用乘方的方式表示第①行数中的第2 016个数;
(2)第②、第③行数与第①行数分别有什么关系?
(3)分别写出每行数的第10个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:

(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由;
(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论;
(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AB上,点F位于边AD上,将纸片沿OE、OF折叠,点B、C、D的对应点分别为B′、C′、D′.
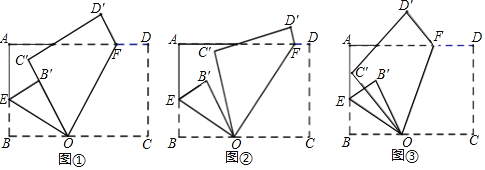
(1)将长方形纸片ABCD按图①所示的方式折叠,若点B′在OC′上,则∠EOF的度数为 ;(直接填写答案)
(2)将长方形纸片ABCD按图②所示的方式折叠,若∠B′OC′=20°,求∠EOF的度数;(写出必要解题步骤)
(3)将长方形纸片ABCD按图③所示的方式折叠,若∠EOF=x°,则∠B′OC′的度数为 .(直接填写答案,答案用含x的代数式表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2所示,当伞收紧时P与A重合,当伞慢慢撑开时,动点P由A向B移动,当点P到达B时,伞张得最开,此时最大张角∠ECF=150°,已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米CE=CF=18.0分米.
(1)求AP长的取值范围;
(2)当∠CPN=60°,求AP的值;
(3)在阳光垂直照射下,伞张得最开时,求伞下的阴影(假定为圆面)面积S.(结果保留![]() )(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
)(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校餐厅计划购买一批餐桌和餐椅,先从甲、乙两个商场了解到:同一型号的餐桌报价每张均为200元,餐椅报价每把均为70元,甲商场规定:每购买一张餐桌赠送一把餐椅;乙商场规定:所有餐桌、餐椅均按报价的八折销售.
(1)学校计划购买15张餐桌和![]() (
(![]() >15)把餐椅,则到甲商场购买所需的费用为 _;到乙商场购买所需的费用为 _.
>15)把餐椅,则到甲商场购买所需的费用为 _;到乙商场购买所需的费用为 _.
(2)若学校计划购进15张餐桌和30把餐椅,请通过计算说明,到哪个商场购买合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣
x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式;
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com