

分析 (1)由两三角形全等以及边角关系,能够找出重叠部分的两条直角边,利用三角形的面积公式即可得出结论;
(2)借助角的三角函数值,可将各边换成含x的代数式,再由边与边的关系即可求出结论;
(3)分成三部分,每部分图形样式不同,画出图形,数形结合,即可得出结论.
解答 解:(1)令AB与DF交点为P,如图1,
∵在△ABC中,∠ACB=90°,BC=3,AC=4,
∴tan∠BAC=$\frac{BC}{AC}$=$\frac{3}{4}$,AB=5,
∵△ABC≌△DEF,
∴EF=BC=3,
∴FP=EF×tan∠BAC=3×$\frac{3}{4}$=$\frac{9}{4}$,
△EFP=$\frac{1}{2}$×EF×FP=$\frac{1}{2}$×3×$\frac{9}{4}$=$\frac{27}{8}$.
故点A与点E重合时两三角形重叠部分的面积为$\frac{27}{8}$.
(2)假设存在,则分两种情况:
①当NM=AM时,过M作MQ⊥AC于Q点,如图2,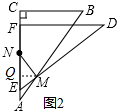
∵在△ABC中,∠ACB=90°,BC=3,AC=4,
∴AB=5(勾股定理),cos∠BAC=$\frac{4}{5}$,
∵NM=AM,MQ⊥AC,
∴AQ=$\frac{1}{2}$AN=AM×cos∠BAC=$\frac{4}{5}$x,
∵点N是线段AC的中点,
∴AN=$\frac{1}{2}$AC=2,
∴有$\frac{4}{5}$x=1,解得x=$\frac{5}{4}$.
②当NM=AN时,过M作MQ1⊥AC于Q1点,如图3,
∵AM=x,∠ACB=90°,BC=3,AC=4,
∴MQ1=$\frac{3}{5}$x,AQ1=$\frac{4}{5}$x,
∵AN=2,
∴NQ1=AQ1-AN=$\frac{4}{5}$x-2,
在直角△NMQ1中,由勾股定理,得${(\frac{3}{5}x)}^{2}$+${(\frac{4}{5}x-2)}^{2}$=22,
即x2-$\frac{16}{5}$x=0,解得x=0(舍去)或x=$\frac{16}{5}$.
结合①②得知,两种情况下,点E都没有运动到N点,故在△DEF运动过程中,△AMN能是以MN为腰的等腰三角形,此时x的值为$\frac{5}{4}$或$\frac{16}{5}$.
(3)①当F点在线段AC上时(同图2),令DF与AB交于R点
此时有MQ=$\frac{3}{5}$x,AQ=$\frac{4}{5}$x,QE=$\frac{3}{4}$MQ=$\frac{9}{20}$x,AE=AQ-QE=$\frac{7}{20}$x,
∵F点在线段AC上,
∴0≤AE≤AC-EF,即0≤$\frac{7}{20}$x≤1,
∴0≤x≤$\frac{20}{7}$,
AF=AE+EF=$\frac{7}{20}$x+3,FR=$\frac{3}{4}$AF=$\frac{21}{80}$x+$\frac{9}{4}$,
CF=AC-AF=1-$\frac{7}{20}$x,
y=$\frac{1}{2}$×AB×BC-$\frac{1}{2}$×AE×MQ-$\frac{1}{2}$×(FR+BC)×CF=$\frac{27}{8}$+$\frac{63x}{80}$-$\frac{147{x}^{2}}{3200}$(0≤x≤$\frac{20}{7}$).
②当F点在线段AC延长线上,且M点在线段AB上,(同图3)此时$\frac{20}{7}$<x≤5,
MQ1=$\frac{3}{5}$x,AQ1=$\frac{4}{5}$x,CQ1=AC-AQ1=4-$\frac{4}{5}$x,EQ1=$\frac{3}{4}$MQ1=$\frac{9}{20}$x,
y=$\frac{1}{2}$•EQ1•MQ1+$\frac{1}{2}$•(MQ1+BC)•CQ1=6-$\frac{69}{200}$•x2($\frac{20}{7}$<x≤5).
③当M点在线段AB延长线上,且E点不超过N点,如图4,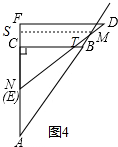
过M作MS⊥AC交AC延长线于S点,令DE与BC交点为T点,
MS=$\frac{3}{5}$x,SA=$\frac{4}{5}$x,SE=$\frac{3}{4}$MS=$\frac{9}{20}$x,AE=SA-SE=$\frac{7}{20}$x,CE=AC-AE=4-$\frac{7}{20}$x,CT=$\frac{4}{3}$CE=$\frac{16}{3}$-$\frac{7}{15}$x,
当N、E重合时,有AE=AN=2,即$\frac{7}{20}$x=2,解得x=$\frac{40}{7}$,
y=$\frac{1}{2}$•CE•CT=$\frac{32}{3}$-$\frac{28}{15}$x+$\frac{49}{600}$x2(5<x≤$\frac{40}{7}$).
综合①②③得知y=$\left\{\begin{array}{l}{\frac{27}{8}+\frac{63}{80}x-\frac{147}{3200}{x}^{2}(0≤x≤\frac{20}{7})}\\{6-\frac{69}{200}{x}^{2}(\frac{20}{7}<x≤5)}\\{\frac{32}{3}-\frac{28}{15}x+\frac{49}{600}{x}^{2}(5<x≤\frac{40}{7})}\end{array}\right.$.
点评 本题考查了三角形的面积、三角函数以及勾股定理等知识,解题的关键是画出图形,利用数形结合即可方便快速的解决问题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2x+2 | B. | y=2x-5 | C. | y=2x+1 | D. | y=2x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| z(元/m2) | 50 | 52 | 54 | 56 | 58 | … |
| x(年) | 1 | 2 | 3 | 4 | 5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
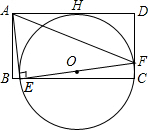 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,∠AFE=30°,△ECF的外接圆切AD于H,则sin∠DAF=$\frac{3}{14}\sqrt{3}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,∠AFE=30°,△ECF的外接圆切AD于H,则sin∠DAF=$\frac{3}{14}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由7x=4x-3移项得7x-4x=3 | |
| B. | 由$\frac{2x-1}{3}=1+\frac{x-3}{2}$去分母得2(2x-1)=1+3(x-3) | |
| C. | 由2(2x-1)-3(x-3)=1去括号得4x-2-3x-9=1 | |
| D. | 由2x+1=x+7移项,合并同类项得x=6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com