
 已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.
已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.分析 (1)由∠ABD=∠CBD,DE∥BC 可推得∠EDB=∠CBD,进而推出∠ABD=∠EDB,由此可得BE=DE=6,由DE∥BC 可得$\frac{AE}{EB}=\frac{AD}{DC}=\frac{1}{3}$,进而证得AE=2,于是可得结论;
(2)△ADE看成以DE为底,高为h1,△BCD看成以BC为底,高为h2,由平行线分线段成比例定理和相似三角形的性质可得$\frac{{h}_{1}}{{h}_{2}}$=$\frac{AD}{DE}=\frac{1}{3}$,$\frac{DE}{BC}=\frac{1}{4}$,进而证得结论.
解答  解:(1)BD平∠ABC,
解:(1)BD平∠ABC,
∴∠ABD=∠CBD,
∵DE∥BC,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴BE=DE=6,
∵DE∥BC,
∴$\frac{AE}{EB}=\frac{AD}{DC}=\frac{1}{3}$,
∴$\frac{AE}{6}=\frac{1}{3}$,
∴AE=2,
∴AB=AE+BE=8;
(2)△ADE看成以DE为底,高为h1,△BCD看成以BC为底,高为h2,
∵DE∥CB,
∴△AED~△ABC,
∴$\frac{{h}_{1}}{{h}_{2}}$=$\frac{AD}{DE}=\frac{1}{3}$,$\frac{DE}{BC}=\frac{1}{4}$,
∴$\frac{{S}_{△ADE}}{{S}_{△BCD}}=\frac{\frac{1}{2}DE•{h}_{1}}{\frac{1}{2}BC•{h}_{2}}=\frac{1}{12}$.
点评 本题主要考查了等腰三角形的性质,平行线分线段成比例定理和相似三角形的性质,三角形的面积等知识,熟练应用平行线分线段成比例定理和相似三角形的性质是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | ∠D=40°,∠E=80°,∠A=60°,∠B=80° | |
| B. | ∠A=∠D,AB:AC=DF:EF | |
| C. | ∠B=∠E=90°,BC:EF=AC:DF | |
| D. | AB=1,BC=2,CA=1.5,DE=6,EF=4,FD=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
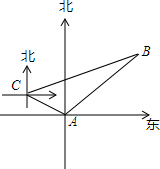 如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时$15\sqrt{2}$千米的速度沿北偏西60°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船加快速度(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时$15\sqrt{2}$千米的速度沿北偏西60°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船加快速度(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
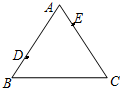 如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.
如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com