
 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:分析 根据正方形及旋转的性质,可得出△HAE和△BGE均为直角边为$\sqrt{2}$-1的等腰直角三角形,即AE=GE,在△AED和△GED中由三条边都相等,可利用全等三角形的判定定理(SSS)证出△AED≌△GED(②正确),根据全等三角形的性质可得出∠AED=∠GED=67.5°,在△AEF中利用三角形内角和定理可得出∠AFE=67.5°=∠AEF,从而得出AF=AE,结合AF⊥BD、EG⊥BD及AE=GE可得出四边形AEGF为菱形(①正确);由邻补角互补结合∠EFG的度数可求出∠DFG=112.5°(③不正确);根据菱形的性质可得出FG=EG=$\sqrt{2}$-1,进而可得出BC+FG=$\sqrt{2}$(④正确).综上即可得出结论.(对于填空题来说,结合图形及正方形的性质可直接得出正确的结论为①②④)
解答 解:∵正方形ABCD的边长为1,
∴∠BCD=∠BAD=90°,∠CBD=45°,BD=$\sqrt{2}$,AD=CD=1.
由旋转的性质可知:∠HGD=BCD=90°,∠H=∠CBD=45°,BD=HD,GD=CD,
∴HA=BG=$\sqrt{2}$-1,∠H=∠EBG=45°,∠HAE=∠BGE=90°,
∴△HAE和△BGE均为直角边为$\sqrt{2}$-1的等腰直角三角形,
∴AE=GE.
在△AED和△GED中,$\left\{\begin{array}{l}{AE=GE}\\{AD=GD=1}\\{ED=ED}\end{array}\right.$,
∴△AED≌△GED(SSS)(②正确),
∴∠AED=∠GED=$\frac{1}{2}$(180°-∠BEG)=67.5°,
∴∠AFE=180°-∠EAF-∠AEF=180°-45°-67.5°=67.5°=∠AEF,
∴AE=AF.
∵AE=GE,AF⊥BD,EG⊥BD,
∴AF=GE且AF∥GE,
∴四边形AEGF为平行四边形.
∵AE=GE,
∴平行四边形AEGF是菱形(①正确).
∵四边形AEGF是菱形,
∴∠EFG=∠GEF=67.5°,FG=EG=$\sqrt{2}$-1,
∴∠DFG=180°-∠DFG=112.5°(③不正确),BC+FG=1+$\sqrt{2}$-1=$\sqrt{2}$(④正确).
综上所述:正确的结论有①②④.
故答案为:①②④.
点评 本题考查了全等三角形的判定与性质、旋转的性质、菱形的判定及性质、正方形的性质以及邻补角,逐一分析四条结论的正误是解题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
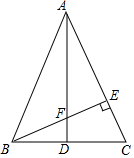 如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
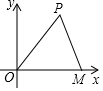 如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM.
如图,在平面直角坐标系中,点M(14,0)是x轴上的点,点P的坐标是(9,12),连接OP,PM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移5单位 | B. | 向左平移3单位 | C. | 向右平移1单位 | D. | 向右平移2单位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
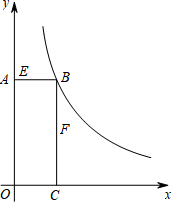 如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.
如图,矩形AOCB的顶点B在反比例函数$y=\frac{k}{x}(k>0$,x>0)的图象上,且AB=3,BC=8.若动点E从A开始沿AB向B以每秒1个单位长度的速度运动,同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动,设运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com