
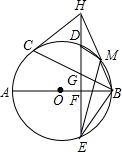
 如图,AB、BC分别是⊙O的直径和弦,点D为$\widehat{BC}$上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD、ME、BE.求证:
如图,AB、BC分别是⊙O的直径和弦,点D为$\widehat{BC}$上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD、ME、BE.求证:分析 ①直接利用圆内接四边形的性质得出∠DMB+∠BMD=180°,进而得出答案;
②连接OC,利用切线的性质,进而证明∠BFG=∠OCH=90°即可得出答案;
③利用圆内接四边形的性质,结合三角形外角的性质,证明∠HMD=∠DEB=∠EMB即可.
解答 证明:①∵四边形DEBM是⊙O的内接四边形,
∴∠DMB+∠BMD=180°,
∵∠HMD+∠BMD=180°,
∴∠BED=∠HMD;
②连接OC,
∵HC=HG,
∴∠HCG=∠HGC;
∵HC切⊙O于C点,
∴∠OCB+∠HCG=90°;
∵OB=OC,
∴∠OCB=∠OBC,
∵∠HGC=∠BGF,
∴∠OBC+∠BGF=90°,
∴∠BFG=90°,即DE⊥AB;
③由②知DE⊥AB,
∵AB是⊙O的直径,
∴$\widehat{BD}$=$\widehat{BE}$,
∴∠BED=∠BME;
∵四边形BMDE内接于⊙O,
∴∠HMD=∠BED,
∴∠HMD=∠BME;
∵∠BME是△HEM的外角,
∴∠BME=∠MHE+∠MEH,
∴∠HMD=∠MHE+∠MEH.
点评 此题主要考查了切线的性质、三角形的内角和外角的性质、等腰三角形的性质、内接四边形的性质等知识,熟练应用圆内接四边形的性质是解题关键.


科目:初中数学 来源: 题型:选择题
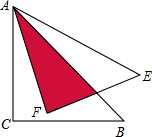 如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )
如图,将等腰直角三角形ABC绕点A逆时针旋转15度得到△AEF,若AC=$\sqrt{3}$,则阴影部分的面积为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
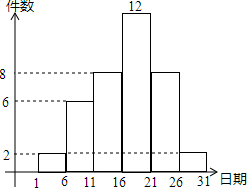 在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.
在学校开展的综合实践活动中,八年级某班对本班的40名学生进行了小制作评比,作品上交时间为5月1日至31日,评委把同学们上交作品的件数按5天一组分组统计,绘制了频数直方图(如图),图中从左到右依次为第一、二、三、四、五、六组.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
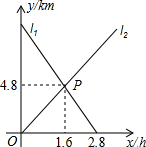 小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系,则小敏、小聪行走的速度分别是( )
小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间xh之间的关系,则小敏、小聪行走的速度分别是( )| A. | 3km/h和4km/h | B. | 3km/h和3km/h | C. | 4km/h和4km/h | D. | 4km/h和3km/h |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和小芳做一个“配色”的游戏,下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.
小明和小芳做一个“配色”的游戏,下图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色.同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com