
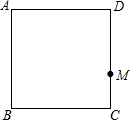
 如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.
如图,在正方形ABCD中,点M在CD边上,点N在正方形ABCD外部,且满足∠CMN=90°,CM=MN.连接AN,CN,取AN的中点E,连接BE,AC,交于F点.分析 (1)①依照题意补全图形即可;②连接CE,由正方形以及等腰直角三角形的性质可得出∠ACD=∠MCN=45°,从而得出∠ACN=90°,再根据直角三角形的性质以及点E为AN的中点即可得出AE=CE,由此即可得出B、E在线段AC的垂直平分线上,由此即可证得BE⊥AC;
(2)BE=$\frac{{\sqrt{2}}}{2}$AD+$\frac{1}{2}$CN.根据正方形的性质可得出BF=$\frac{{\sqrt{2}}}{2}$AD,再结合三角形的中位线性质可得出EF=$\frac{1}{2}$CN,由线段间的关系即可证出结论;
(3)找出EN所扫过的图形为四边形DFCN.根据正方形以及等腰直角三角形的性质可得出BD∥CN,由此得出四边形DFCN为梯形,再由AB=1,可算出线段CF、DF、CN的长度,利用梯形的面积公式即可得出结论.
解答 解:(1)①依题意补全图形,如图1所示.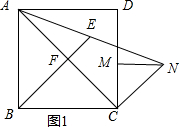
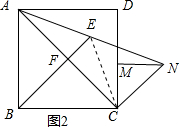
②证明:连接CE,如图2所示.
∵四边形ABCD是正方形,
∴∠BCD=90°,AB=BC,
∴∠ACB=∠ACD=$\frac{1}{2}$∠BCD=45°,
∵∠CMN=90°,CM=MN,
∴∠MCN=45°,
∴∠ACN=∠ACD+∠MCN=90°.
∵在Rt△ACN中,点E是AN中点,
∴AE=CE=$\frac{1}{2}$AN.
∵AE=CE,AB=CB,
∴点B,E在AC的垂直平分线上,
∴BE垂直平分AC,
∴BE⊥AC.
(2)BE=$\frac{{\sqrt{2}}}{2}$AD+$\frac{1}{2}$CN.
证明:∵AB=BC,∠ABE=∠CBE,
∴AF=FC.
∵点E是AN中点,
∴AE=EN,
∴FE是△ACN的中位线.
∴FE=$\frac{1}{2}$CN.
∵BE⊥AC,
∴∠BFC=90°,
∴∠FBC+∠FCB=90°.
∵∠FCB=45°,
∴∠FBC=45°,
∴∠FCB=∠FBC,
∴BF=CF.
在Rt△BCF中,BF2+CF2=BC2,
∴BF=$\frac{{\sqrt{2}}}{2}$BC.
∵四边形ABCD是正方形,
∴BC=AD,
∴BF=$\frac{{\sqrt{2}}}{2}$AD.
∵BE=BF+FE,
∴BE=$\frac{{\sqrt{2}}}{2}$AD+$\frac{1}{2}$CN.
(3)在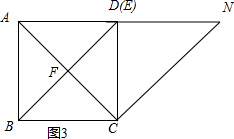 点M沿着线段CD从点C运动到点D的过程中,线段EN所扫过的图形为四边形DFCN.
点M沿着线段CD从点C运动到点D的过程中,线段EN所扫过的图形为四边形DFCN.
∵∠BDC=45°,∠DCN=45°,
∴BD∥CN,
∴四边形DFCN为梯形.
∵AB=1,
∴CF=DF=$\frac{1}{2}$BD=$\frac{\sqrt{2}}{2}$,CN=$\sqrt{2}$CD=$\sqrt{2}$,
∴S梯形DFCN=$\frac{1}{2}$(DF+CN)•CF=$\frac{1}{2}$($\frac{\sqrt{2}}{2}$+$\sqrt{2}$)×$\frac{\sqrt{2}}{2}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 本题考查了正方形的性质、等腰直角三角形的性质、平行线的性质以及梯形的面积公式,解题的关键是:(1)根据垂直平分线上点的性质证出垂直;(2)用AD表示出EF、BF的长度;(3)找出EN所扫过的图形.本题属于中档题,难度不小,解决该题型题目时,根据题意画出图形,利用数形结合解决问题是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=50}\\{10(x+y)=320}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=50}\\{6x+10y=320}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=50}\\{6x+y=320}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=50}\\{10x+6y=320}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{a}{5}}$ | C. | $\sqrt{8a}$ | D. | $\sqrt{10a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (8+3a-2b)(8-3a-2b) | B. | (8+3a+2b)(8-3a-2b) | C. | (8+3a+2b)(8-3a+2b) | D. | (8+3a-2b)(8-3a+2b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com