
【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长。
的长。
【答案】解:(1)如图,连接AE,
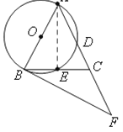
∵AB是⊙O的直径,
∴∠AEB=900,即AE⊥BC。
又∵AB=AC,∴BE=CE。
(2)∵∠BAC=540,AB=AC,∴∠ABC=630。
又∵BF是⊙O的切线,∴∠ABF=900。
∴∠CBF=∠ABF一∠ABC=270。
(3)连接OD,
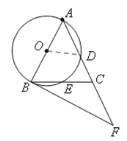
∵OA=OD,∠BAC=540,∴∠AOD=720。
又∵AB=6,∴OA=2。
∴![]() 。
。
【解析】(1)连接AE,则根据直径所对圆周角是直角的性质得AE⊥BC,从而根据等腰三角形三线合一的性质得出结论。
(2)由∠BAC=540,AB=AC,根据等腰三角形等边对等角的性质和三角形内角和等于零180度求得∠ABC=630;由切线垂直于过切点直径的性质得∠ABF=900,从而由∠CBF=∠ABF一∠ABC得出结论。
(3)连接OD,根据同弧所对圆周角是圆心角一半的性质,求得∠AOD=720,根据弧长公式即可求。


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】操作与证明:

如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是: ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,点E,F分别是BC,DC上的动点.沿EF 折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,求CF的取值范围.
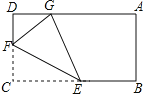
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB=CD,E,F分别为边BC与AD的中点,AE∥CD,延长BA,CD,分别与EF的延长线交于点G,H,连接AH,ED.
(1)求证:AH∥ED;
(2)求证:AE=AG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进货价每个10元的商品按售价18元售出时,每天可卖出60个.商店经理到市场上做了一番调查后发现,若将这种商品的售价每提高1元,则日销售量就减少5个;若将这种商品的售价每降低1元,则日销售量就增加10个。为获得每日最大利润,此商品售价应定为每个多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用a小时清点完一批图书的一半,小强加入清点另一半图书的工作,两人合作![]() 小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
小时清点完另一半图书.设小强单独清点完这批图书需要x小时.
(1)若a=3,求小强单独清点完这批图书需要的时间.
(2)请用含a的代数式表示x,并说明a满足什么条件时x的值符合实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上的一动点,连接AC并延长交⊙O于D,过点D作直线交OB延长线于E,且DE=CE,已知OA=8.
(1)求证:ED是⊙O的切线;
(2)当∠A=30°时,求CD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com