
【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.
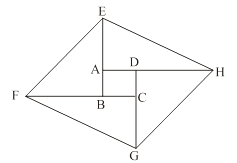
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
【答案】
(1)
证明:在矩形ABCD中,AD=BC,∠BAD=∠BCD=90°.
又∵BF=DH,
∴AD+DH=BC+BF
即AH=CF.
在Rt△AEH中,EH=![]() .
.
在Rt△CFG中,FG=![]() .
.
∵AE=CG,
∴EH=FG.
同理得,EF=HG.
∴四边形EFGH为平行四边形.
(2)
解:在正方形ABCD中,AB=AD=1.
设AE=x,则BE=x+1.
∵在Rt△BEF中,∠BEF=45°.
∴BE=BF.
∵BF=DH,
∴DH=BE=x+1.
∴AH=AD+DH=x+2.
∵在Rt△AEH中,tan∠AEH=2,
∴AH=2AE.
∴2+x=2x.
∴x=2.
即AE=2.
【解析】(1)在矩形ABCD中,AD=BC,∠BAD=∠BCD=90°.根据BF=DH,得出AH=CF.根据勾股定理 EH=![]() .FG=
.FG=![]() .
.
由AE=CG得出EH=FG.EF=HG;从而证明四边形EFGH为平行四边形.
(2)在正方形ABCD中,AB=AD=1; 设AE=x,则BE=x+1;在Rt△BEF中,∠BEF=45°.得出BE=BF=DH=x+1;AH=AD+DH=x+2.
在Rt△AEH中,利用正切即可求出AE的长.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )
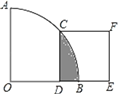
A. 2π﹣8 B. 4π﹣8 C. 2π﹣4 D. 4π﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2 ![]() ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为 ![]() ;
;
其中正确的是(把你认为正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家统计局4月15日发布数据,初步核算,2015年一季度全国国内生产总值为140667亿元,其中数据140667用科学记数法表示为( )
A.1.40667×105
B.1.40667×106
C.14.0667×104
D.0.140667×106
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com