
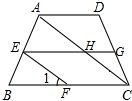
 如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°.
如图,AD∥EG∥BC,AC∥EF,若∠1=50°,则∠AHG=130°. 分析 由平行线的性质可得到∠1=∠HEF=∠AHE=∠GHC=∠HCF=∠DAC,结合∠DAH+∠AHG=180°,可求得∠AHG.
解答 解:∵EF∥AC,
∴∠1=∠HCF,∠FEH=∠AHE,
∵EG∥BC,
∴∠1=∠FEH,∠GHC=∠HCF,
∴AD∥BC,
∴∠DAH=∠HCF,
∴∠1=∠HEF=∠AHE=∠GHC=∠HCF=∠DAC,
∵∠1=50°,
∴∠DAC=∠1=50°,
∵AD∥EG,
∴∠DAC+∠AHG=180°,
∴∠AHG=180°-50°=130°;
故答案为:130.
点评 本题主要考查平行线的性质,掌握平行线的性质是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
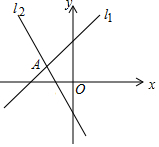 如图,在直角坐标系中,直线l1:y1=kx+b与直线l2:y2═mx+n在第二象限相交于点A(-1,a),则不等式kx+b<mx+n的解集是( )
如图,在直角坐标系中,直线l1:y1=kx+b与直线l2:y2═mx+n在第二象限相交于点A(-1,a),则不等式kx+b<mx+n的解集是( )| A. | x<-1 | B. | x<a | C. | x>-1 | D. | -1<x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 年龄/岁 | 12 | 13 | 14 | 15 |
| 人数/人 | 2 | 4 | 6 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$×$3\sqrt{3}$=6$\sqrt{3}$ | C. | $\sqrt{2}$$÷\sqrt{3}$=$\frac{\sqrt{6}}{3}$ | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com