
如图,已知反比例函数y= 过点P, P点的坐标为(3-m,2m),m是分式方程
过点P, P点的坐标为(3-m,2m),m是分式方程 的解,PA⊥x轴于点A,PB⊥y轴于点B.
的解,PA⊥x轴于点A,PB⊥y轴于点B.
(1)试判断四边形PAOB的形状,并说明理由.
(2)连结AB,E为AB上的一点,EF⊥BP于点F,G为AE的中点,连结OG、FG,试问FG和OG有何数量关系?请写出你的结论并证明.
(3)若M为反比例函数y= 在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
在第三象限内的一动点,过M作MN⊥x轴于交AB的延长线于点N,是否存在一点M使得四边形OMNB为等腰梯形?若存在,请求出M点的坐标;若不存在,请说明理由.
解:(1)四边形PAOB是正方形.理由如下
∵∠AOB=∠OBP=∠OAP=90°
∴四边形PAOB是矩形
m-3+m-2=-3
解得:m=1
经检验知m=1是原分式方程的解
∴P(2,2)
∴PB=PA=2
∴四边形PAOB是正方形.
(2)OG=FG.证明如下:
延长FE交OA于点H,连结GH
∵∠HFB =∠FBO=∠BOH=90°
∴BOHF是矩形
∴BF=OH
∵∠FBE=∠FEB=45°
∴EF= BF=OH
∵∠EHA=90°,G为AE的中点
∴GH=GE=GA
∴∠GEH=∠GAH=45°
∴∠GEF=∠GHO
∴△GEF≌△GHO
∴OG=FG
(3)由题意知:∠BNM=45° 
∵要让四边形OBNM为等腰梯形
∴∠BNM=∠NMO=45°
∴设M点的坐标为(x,x),代入
∴x=±2
∵M是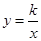 第三象限上一动点
第三象限上一动点
∴x=-2
∴M点的坐标为(-2,-2)
解析


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| m |
| x |
| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y1=
如图,已知反比例函数y1=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知反比例函数y=
如图,已知反比例函数y=| k |
| x |
| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com