
科目:初中数学 来源: 题型:
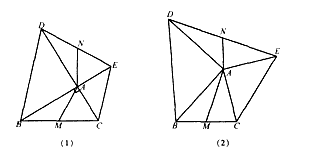
 (2012•浦口区一模)提出问题:
(2012•浦口区一模)提出问题: ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:
 θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.
θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
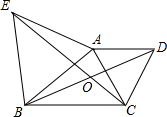 如图,以△ABC的两边AB、AC向外作等边三角形ABE和等边三角形ACD,连接BD、CE,相交于O.
如图,以△ABC的两边AB、AC向外作等边三角形ABE和等边三角形ACD,连接BD、CE,相交于O.查看答案和解析>>
科目:初中数学 来源:2013届北京市八年级上学期期中数学试卷(解析版) 题型:解答题
如图,以△ABC的两边AB、AC向外作等边三角形ABE和等边三角形ACD,连结BD、CE,相交于O.(1)试写出图中和BD相等的一条线段并说明你的理由;(2)求出BD和CE的夹角大小,若改变△ABC的形状,这个夹角的度数会发生变化吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com