
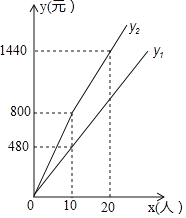
【题目】某景区售票处规定:非节假日的票价打a折售票;节假日根据团队人数x(人)实行分段售票:若x≤10,则按原展价购买;若x>10,则其中10人按原票价购买,超过部分的按原那价打b折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y1元,在节假日的购票款为y2元,y1、y2与x之间的函数图象如图所示.
(1)观察图象可知:a= ,b= ;
(2)当x>10时,求y2与x之间的函数表达式;
(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.
【答案】(1)6,8;(2)y2=64x+160(x>10);(3)甲团有35人,乙团有15人.
【解析】
(1)根据原票价和实际票价可求a、b的值,m的值可看图得到;
(2)先列函数解析式,然后将图中的对应值代入其中求出常数项,即可得到解析式;
(3)分两种情况讨论,即不多于10和多于10人,找出等量关系,列出关于人数的n的一元一次方程,解此可得人数.
(1)门票定价为80元/人,那么10人应花费800元,而从图可知实际只花费480元,是打6折得到的价格,
所以a=6;
从图可知10人之外的另10人花费640元,而原价是800元,可以知道是打8折得到的价格,
所以b=8,
故答案为:6,8
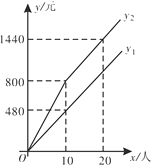
(2)当x>10时,设y2=kx+b.
∵图象过点(10,800),(20,1440),
∴![]()
解得![]()
∴y2=64x+160(x>10)
故答案为:y2=64x+160(x>10)
(3)设甲团有m人,乙团有n人
由图象,得y1=48x,
当m>10时,
依题意,得![]()
解得![]()
答:甲团有35人,乙团有15人.
故答案为:甲团有35人,乙团有15人


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
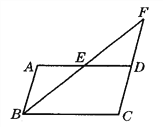
【题目】如图,平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线交于点F.
(1)求证:△ABE≌△DFE;
(2)试连结BD,AF,判断四边形ABDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.



(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,已知抛物线![]() 经过点
经过点![]() ,定点为
,定点为![]() ,对称轴
,对称轴![]() 交
交![]() 轴于点
轴于点![]() .点
.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是在
是在![]() 轴下方的抛物线对称轴上的一个动点,
轴下方的抛物线对称轴上的一个动点,![]() 交
交![]() 于点
于点![]() ,
,![]() 轴交射线
轴交射线![]() 于点
于点![]() ,作直线
,作直线![]() .
.
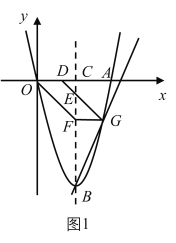
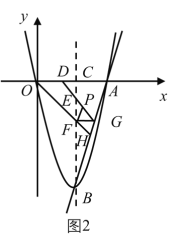
(1)求点![]() 的坐标;
的坐标;
(2)如图1,当点![]() 恰好落在该抛物线上时,求点
恰好落在该抛物线上时,求点![]() 的坐标;
的坐标;
(3)如图2,当![]() 时,判断点
时,判断点![]() 是否在直线
是否在直线![]() 上,说明理由;
上,说明理由;
(4)在(3)的条件下,延长![]() 交
交![]() 于点
于点![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,探究四边形
,探究四边形![]() 是否为平行四边形,并说明理由.
是否为平行四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直升飞机在大桥AB上方C点处测得A,B两点的俯角分别为45°和31°.若飞机此时飞行高度CD为1205m,且点A,B,D在同一条直线上,求大桥AB的长.(精确到1m)(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
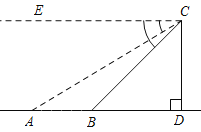
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12,BC=10,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△![]() ,连接
,连接![]() ,则
,则![]() 的最小值是__________.
的最小值是__________.
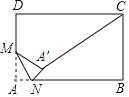
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com