
 ЃЛ
ЃЛЗжЮі ЁОИХФюбЇЯАЁП
ЃЈ1ЃЉЗжБ№АДЙЋЪННјааМЦЫуМДПЩЃЛ
ЃЈ2ЃЉИљОнЖЈвхвРДЮХаЖЈМДПЩЃЛ
ЁОЩюШыЫМПМЁП
ЃЈ1ЃЉАбГ§ЗЈЛЏЮЊГЫЗЈЃЌЕквЛИіЪ§ВЛБфЃЌДгЕкЖўИіЪ§ПЊЪМвРДЮБфЮЊЕЙЪ§ЃЌгЩДЫЗжБ№ЕУГіНсЙћЃЛ
ЃЈ2ЃЉНсЙћЕквЛИіЪ§ВЛБфЮЊaЃЌЕкЖўИіЪ§МАКѓУцЕФЪ§БфЮЊ$\frac{1}{a}$ЃЌдђa?=aЁС$ЃЈ\frac{1}{a}ЃЉ$ ЃЛ
ЃЛ
ЃЈ3ЃЉНЋЕкЖўЮЪЕФЙцТЩДњШыМЦЫуЃЌзЂвтдЫЫуЫГађЃЎ
НтД№ НтЃКЁОИХФюбЇЯАЁП
ЃЈ1ЃЉ2Ђл=2ЁТ2ЁТ2=$\frac{1}{2}$ЃЌ
ЃЈ-$\frac{1}{2}$ЃЉЂн=ЃЈ-$\frac{1}{2}$ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉ=1ЁТЃЈ-$\frac{1}{2}$ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉ=ЃЈ-2ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉЁТЃЈ-$\frac{1}{2}$ЃЉ=-8
ЙЪД№АИЮЊЃК$\frac{1}{2}$ЃЌ-8ЃЛ
ЃЈ2ЃЉAЁЂШЮКЮЗЧСуЪ§ЕФШІ2ДЮЗНОЭЪЧСНИіЯрЭЌЪ§ЯрГ§ЃЌЫљвдЖМЕШгк1ЃЛ ЫљвдбЁЯюAе§ШЗЃЛ
BЁЂвђЮЊЖрЩйИі1ЯрГ§ЖМЪЧ1ЃЌЫљвдЖдгкШЮКЮе§ећЪ§nЃЌ1?ЖМЕШгк1ЃЛ ЫљвдбЁЯюBе§ШЗЃЛ
CЁЂ3Ђм=3ЁТ3ЁТ3ЁТ3=$\frac{1}{9}$ЃЌ4Ђл=4ЁТ4ЁТ4=$\frac{1}{4}$ЃЌдђ 3ЂмЁй4ЂлЃЛ ЫљвдбЁЯюCДэЮѓЃЛ
DЁЂИКЪ§ЕФШІЦцЪ§ДЮЗНЃЌЯрЕБгкЦцЪ§ИіИКЪ§ЯрГ§ЃЌдђНсЙћЪЧИКЪ§ЃЌИКЪ§ЕФШІХМЪ§ДЮЗНЃЌЯрЕБгкХМЪ§ИіИКЪ§ЯрГ§ЃЌдђНсЙћЪЧе§Ъ§ЃЎЫљвдбЁЯюDе§ШЗЃЛ
БОЬтбЁдёЫЕЗЈДэЮѓЕФЃЌЙЪбЁCЃЛ
ЁОЩюШыЫМПМЁП
ЃЈ1ЃЉЃЈ-3ЃЉЂм=ЃЈ-3ЃЉЁТЃЈ-3ЃЉЁТЃЈ-3ЃЉЁТЃЈ-3ЃЉ=ЃЈ-3ЃЉЁС$ЃЈ-\frac{1}{3}ЃЉ^{3}$ЃЛ
5Ђо=5ЁТ5ЁТ5ЁТ5ЁТ5ЁТ5=5ЁС$ЃЈ\frac{1}{5}ЃЉ^{5}$ЃЛ
ЃЈ-$\frac{1}{2}$ЃЉЂт=ЃЈ-$\frac{1}{2}$ЃЉЁС$ЃЈ-\frac{1}{2}ЃЉ^{9}$ЃЛ
ЙЪД№АИЮЊЃКЃЈ-3ЃЉЁС$ЃЈ-\frac{1}{3}ЃЉ^{3}$ЃЛ5ЁС$ЃЈ\frac{1}{5}ЃЉ^{5}$ЃЛЃЈ-$\frac{1}{2}$ЃЉЁС$ЃЈ-\frac{1}{2}ЃЉ^{9}$ЃЛ
ЃЈ2ЃЉa?=aЁС$ЃЈ\frac{1}{a}ЃЉ$ ЃЛ
ЃЛ
ЃЈ3ЃЉ122ЁТЃЈ-$\frac{1}{3}$ЃЉЂмЁСЃЈ-2ЃЉЂн-ЃЈ-$\frac{1}{3}$ЃЉЂоЁТ33ЃЌ
=144ЁТ[ЃЈ-$\frac{1}{3}$ЃЉЁСЃЈ-3ЃЉ3]ЁС[ЃЈ-2ЃЉЁСЃЈ-$\frac{1}{2}$ЃЉ4]-[ЃЈ-$\frac{1}{3}$ЃЉЁСЃЈ-3ЃЉ5]ЁТ33ЃЌ
=144ЁТ9ЁС$ЃЈ-\frac{1}{2}ЃЉ^{3}$-ЃЈ-3ЃЉ4ЁТ33ЃЌ
=16ЁСЃЈ-$\frac{1}{8}$ЃЉ-3ЃЌ
=-2-3ЃЌ
=-5ЃЎ
ЕуЦР БОЬтЪЧгаРэЪ§ЕФЛьКЯдЫЫуЃЌвВЪЧвЛИіаТЖЈвхЕФРэНтгыдЫгУЃЛвЛЗНУцПМВщСЫгаРэЪ§ЕФГЫГ§ЗЈМАГЫЗНдЫЫуЃЌСэвЛЗНУцвВПМВщСЫбЇЩњЕФдФЖСРэНтФмСІЃЛзЂвтЃКИКЪ§ЕФЦцЪ§ДЮЗНЮЊИКЪ§ЃЌИКЪ§ЕФХМЪ§ДЮЗНЮЊе§Ъ§ЃЌЭЌЪБвВвЊзЂвтЗжЪ§ЕФГЫЗНвЊМгРЈКХЃЌЖдаТЖЈвхЃЌЦфЪЕОЭЪЧЖрИіЪ§ЕФГ§ЗЈдЫЫуЃЌвЊзЂвтдЫЫуЫГађЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
 ШчЭМЃЌдкЫФБпаЮABCDжаЃЌЕуEЃЌFЃЌGЃЌHЗжБ№ЪЧADЃЌBDЃЌBCЃЌCAЕФжаЕуЃЌШєЫФБпаЮEFGHЪЧОиаЮЃЌдђЫФБпаЮABCDашТњзуЕФЬѕМўЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкЫФБпаЮABCDжаЃЌЕуEЃЌFЃЌGЃЌHЗжБ№ЪЧADЃЌBDЃЌBCЃЌCAЕФжаЕуЃЌШєЫФБпаЮEFGHЪЧОиаЮЃЌдђЫФБпаЮABCDашТњзуЕФЬѕМўЪЧЃЈЁЁЁЁЃЉ| AЃЎ | ABЁЭDC | BЃЎ | AC=BD | CЃЎ | ACЁЭBD | DЃЎ | AB=DC |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
 ШчЭМЃЌвбжЊOA=OBЃЎдђЪ§жсЩЯЕуAЫљБэЪОЕФЪ§aЪЧ-$\sqrt{10}$ЃЛ
ШчЭМЃЌвбжЊOA=OBЃЎдђЪ§жсЩЯЕуAЫљБэЪОЕФЪ§aЪЧ-$\sqrt{10}$ЃЛВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
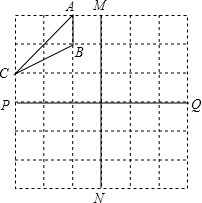 вбжЊЃКШчЭМЁїABCЃЎ
вбжЊЃКШчЭМЁїABCЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
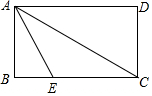 ШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌЕуEдкBCЩЯЃЌЧвAE=EC=2ЃЎШєНЋжНЦЌбиAEелЕўЃЌЕуBКУТфдкACЩЯЃЌдђACЕШгкЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌЕуEдкBCЩЯЃЌЧвAE=EC=2ЃЎШєНЋжНЦЌбиAEелЕўЃЌЕуBКУТфдкACЩЯЃЌдђACЕШгкЃЈЁЁЁЁЃЉ| AЃЎ | 3 | BЃЎ | 2$\sqrt{2}$ | CЃЎ | 2$\sqrt{3}$ | DЃЎ | $\frac{3\sqrt{3}}{2}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com