
【题目】如图,在△ABC中,AB=AC,∠A=40°,D、E分别是AB、AC上的不动点,且BD+CE=BC,点P是BC上一动点,
(1)当PC=CE时,试求∠DPE的度数
(2)当PC=BD时,∠DPE的度数还会与(1)的结果相同吗?若相同请写出求解过程,若不相同,请说明理由

【答案】(1)70°;(2)相同,理由详见解析
【解析】
(1)根据AB=AC,∠A=40°,可求得∠B和∠C,因为BD+CE=BC,PC=CE,可推得BD=BP,即可求得∠BPD和∠CPE度数,可得出∠DPE度数.
(2)若PC=BD,已知BD+CE=BC,可得BP=CE,证明△BDP和△CPE全等,推出∠BDP=∠CPE,∠DPC=∠DPE+∠CPE=∠B+∠BDP,即可求出∠DPE度数.
(1)∵AB=AC,∠A=40°
∴∠B=∠C=(180°-40°)÷2=70°
∵BD+CE=BC,PC=CE
∴BD=BP
∴∠BPD=∠CPE=55°
∴∠DPE=180°-55°×2=70°.
故答案为: 70°
(2)相同,PC=BD时,BD+CE=BC,则BP=CE
在△BDP和△CPE中

△BDP≌△CPE(SAS)
∠BDP=∠CPE,∠DPC=∠DPE+∠CPE=∠B+∠BDP
∴∠DPE=70°
故答案为:相同,理由见解析


科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张,不放回,再从剩下的卡片中随机抽取一张.
(1)请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果,(卡片用A,B,C,D表示);
(2)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(0,0),B(0,4),C(3,t+4),D(3,t). 记N(t)为![]() ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
A. 6、7B. 7、8C. 6、7、8D. 6、8、9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照有关规定,距高铁轨道![]() 米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形
米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形![]() 为一新建小区,直线
为一新建小区,直线![]() 为高铁轨道,
为高铁轨道,![]() 是直线
是直线![]() 上的两点,点
上的两点,点![]() 在一条直线上,且
在一条直线上,且![]() .小王看中了
.小王看中了![]() 号楼
号楼![]() 单元的一套住宅,与售楼人员的对话如下:
单元的一套住宅,与售楼人员的对话如下:
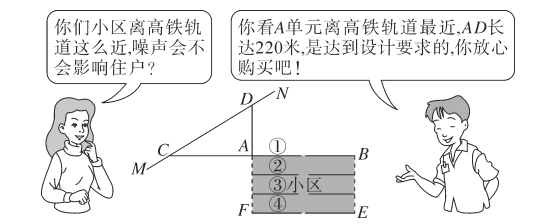
![]() 小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
![]() 若一列长度为
若一列长度为![]() 米的高铁以
米的高铁以![]() 千米/时的速度通过,则
千米/时的速度通过,则![]() 单元用户受到影响的时间有多长?
单元用户受到影响的时间有多长?
(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“丰收1号”小麦的试验田是边长为![]() 米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(
米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(![]() )米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
)米的正方形,两块试验田里的小麦都收获了500千克.(1)哪种小麦的单位面积产量高?(2)高的单位面积产量是低的单位面积产量的多少倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和CEFG的边长分别为m、n,那么△AEG的面积的值( )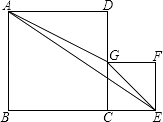
A.与m、n的大小都有关
B.与m、n的大小都无关
C.只与m的大小有关
D.只与n的大小有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从1、2、3、4中任取一个数作为十位上的数字,再从余下的数字中任取一个数作为个位上的数字,那么组成的两位数是6的倍数的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() (x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(x+2)(x﹣4)与x轴交于点A,B(点A位于点B的左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A,B,C的坐标;
(2)设动点N(﹣2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上一点,请你探究:是否存在点P,使以P,A,B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com