
如图,已知正三角形ABC的边长为2a.
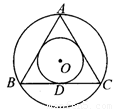
(1)求它的内切圆与外接圆组成的圆环的面积;
(2)根据计算结果,要求圆环的面积,只需测量哪一条弦的大小就可算出圆环的面积;
(3)将条件中的“正三角形”改为“正方形”“正六边形”,你能得出怎样的结论?
(4)已知正n边形的边长为2a,请写出它的内切圆与外接圆组成的圆环面积.
(1)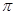 a2;(2)弦AB或BC或AC;
a2;(2)弦AB或BC或AC;
(3)圆环的面积均为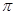 ·(
·(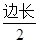 )2;(4)
)2;(4)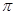 a2
a2
【解析】
试题分析:正多边形的边心距,半径,边长的一半正好构成直角三角形,根据勾股定理就可以求解.
(1)设正三角形ABC的中心为O,BC切⊙O于点D连接OB、OD,
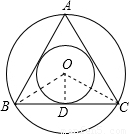
则OD⊥BC,BD=DC=a;
则S圆环=π•OB2-π•OD2=π(OB2-OD2)=π• BD2 =πa2.
(2)只需测出弦BC的长(或AC,AB).
(3)结果一样,即S圆环=πa2
(4)S圆环=πa2.
考点:本题考查的是正多边形的内切圆与外接圆,勾股定理
点评:正多边形的计算,一般是过中心作边的垂线,连接半径,把内切圆半径,外接圆半径和高,中心角之间的计转化为解直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
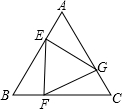 如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )
如图,已知正三角形ABC的边长为1,E,F,G分别是AB,BC,CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是( )A、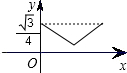 | B、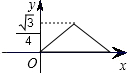 | C、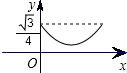 | D、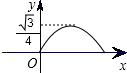 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 29、如图,已知正三角形的边长2a
29、如图,已知正三角形的边长2a查看答案和解析>>
科目:初中数学 来源: 题型:
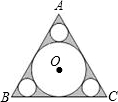 如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为
如图,已知正三角形ABC的边长为6,在△ABC中作内切圆O及三个角切圆(我们把与角两边及三角形内切圆都相切的圆叫角切圆),则△ABC的内切圆O的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 点A运动.
点A运动.查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com