
【题目】在菱形ABCD中,P是AB上一动点(但不与A、B两点重合),DP的延长线交CB延长线于点E.
(1)△APD与△BPE是否总相似,为什么?
(2)当P为AB中点时,求证:点B是EC中点.
(3)当PD⊥AB时,设AD=10,sinA=![]() ,求BE的长.
,求BE的长.

【答案】(1)相似.理由见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)由四边形ABCD为菱形,得到AD∥BC,即可得到结论;(2)先由角角边证得△APD≌△BPE,AD=BE,再由四边形ABCD为菱形, 得到AD=BC,即BE=BC,即点B为EC中点.(3)再Rt△APD中,由AD=10,sinA=![]() 得PD=8,AP=6,故PB=4,由△APD∽△BPE可得
得PD=8,AP=6,故PB=4,由△APD∽△BPE可得![]() =
=![]() ,即可求得BE长.
,即可求得BE长.
试题解析:: (1)相似.
∵四边形ABCD为菱形,
∴AD∥BC.
∴∠DAP=∠EBP,∠ADP=∠BEP.
∴△APD△BPE.
(2)∵P是AB中点,
∴AP=BP.
又∵∠DAP=∠EBP,∠ADP=∠BEP,
∴△APD≌△BPE.
∴AD=BE.
∵四边形ABCD为菱形,
∴AD=BC.
∴BE=BC.
即点B为EC中点.
(3)∵PD⊥AB,AD=10,sinA=![]() . ∴PD=8.∴AP=6.∴PB=AB—AP=10—6=4.
. ∴PD=8.∴AP=6.∴PB=AB—AP=10—6=4.
∵△APD∽△BPE,∴ ![]() =
=![]() ∴BE=
∴BE=![]() =
=![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) 
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个几何体的正视图和左视图.
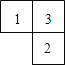
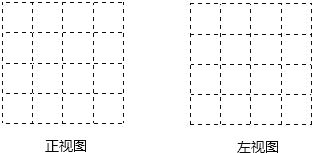
(2)根据三视图,请你求出这个组合几何体的表面积(包括底面积).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】采摘茶叶是茶农一项很繁重的劳动,利用单人便携式采茶机能大大提高生产效率.实践证明,一台采茶机每天可采茶60公斤,是人手工采摘的5倍,购买一台采茶机需2400元.茶园雇人采摘茶叶,按每采摘1公斤茶叶m元的标准支付雇工工资,一个雇工手工采摘茶叶20天获得的全部工钱正好购买一台采茶机.
(1)求m的值;
(2)有两家茶叶种植户王家和顾家均雇人采摘茶叶,王家雇用的人数是顾家的2倍.王家所雇的人中有![]() 的人自带采茶机采摘,
的人自带采茶机采摘, ![]() 的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E,F分别为正方形ABCD的边BC,CD上的点,AF,DE相交于点G,当E,F分别为边BC,CD的中点时,有:①AF=DE;②AF⊥DE成立.
试探究下列问题:
(1)如图1,若点E不是边BC的中点,F不是边CD的中点,且CE=DF,上述结论①,②是否仍然成立?(请直接回答“成立”或“不成立”),不需要证明)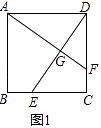
(2)如图2,若点E,F分别在CB的延长线和DC的延长线上,且CE=DF,此时,上述结论①,②是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由;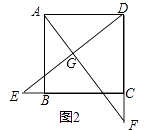
(3)如图3,在(2)的基础上,连接AE和EF,若点M,N,P,Q分别为AE,EF,FD,AD的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种,并证明你的结论.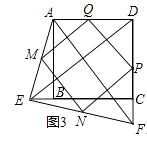
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,a),B(1,b),C(3,c)是抛物线y=x2﹣2x+2上的三点,则a,b,c的大小关系为( )
A.a>c>bB.b>a>cC.c>a>bD.b>c>a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com