
 的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.
的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.| MP |
| BD |
| AP |
| AB |
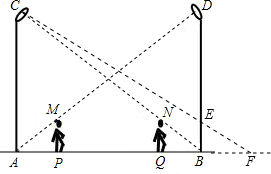 解:(1)由对称性可知AP=BQ,设AP=BQ=xm
解:(1)由对称性可知AP=BQ,设AP=BQ=xm| MP |
| BD |
| AP |
| AB |
| 1.6 |
| 9.6 |
| x |
| 2x+12 |
| BE |
| AC |
| BF |
| FA |
| 1.6 |
| 9.6 |
| y |
| y+18 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
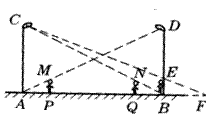
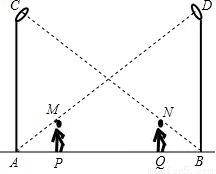
如图,王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶
部刚好接触路灯AC的底部,当他向前再步行12 m到达Q点时,发现身前他影子的顶部
刚好接触到路灯BD的底部,已知王华同学的身高是1.6m,两个路灯的高度都是9.6m。
(1)求两个路灯之间的距离;
(2)当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
查看答案和解析>>
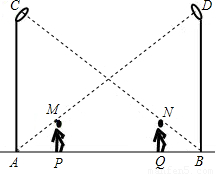
科目:初中数学 来源:第27章《相似》常考题集(19):27.2 相似三角形(解析版) 题型:解答题
查看答案和解析>>
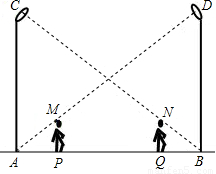
科目:初中数学 来源:2011-2012学年沪科版九年级(上)期末复习数学试卷(二)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:《第24章 图形的相似》2009年单元测验(2)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com