
 ÈçÍŒŁŹ”ăP1Łšx1ŁŹy1Ł©ŁŹ”ăP2Łšx2ŁŹy2Ł©ŁŹĄŁŹ”ăPnŁšxnŁŹynŁ©ÔÚșŻÊę$y=\frac{1}{x}$ŁšxŁŸ0Ł©”ÄÍŒÏóÉÏŁŹĄśP1OA1ŁŹĄśP2A1A2ŁŹĄśP3A2A3ŁŹĄŁŹĄśPnAn-1An¶ŒÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹĐ±±ßOA1ĄąA1A2ĄąA2A3ŁŹĄŁŹAn-1An¶ŒÔÚxÖáÉÏŁšnÊÇŽóÓÚ»ò”ÈÓÚ2”ÄŐęŐûÊ꣩ŁŹÈôĄśP1OA2”ÄÄÚœÓŐę·œĐÎB1C1D1E2”ÄÖÜł€ŒÇÎȘl1ŁŹĄśP2A1A2”ÄÄÚœÓŐę·œĐÎB2C2D2E2”ÄÖÜł€ŒÇÎȘl2ŁŹĄŁŹĄśPnAn-1An”ÄÄÚœÓŐę·œĐÎBnCnDnEn”ÄÖÜł€ŒÇÎȘlnŁŹÔòÓĂșŹn”ÄÊœŚÓ±íÊŸl1+l2+l3+Ą+lnÎȘŁšĄĄĄĄŁ©
ÈçÍŒŁŹ”ăP1Łšx1ŁŹy1Ł©ŁŹ”ăP2Łšx2ŁŹy2Ł©ŁŹĄŁŹ”ăPnŁšxnŁŹynŁ©ÔÚșŻÊę$y=\frac{1}{x}$ŁšxŁŸ0Ł©”ÄÍŒÏóÉÏŁŹĄśP1OA1ŁŹĄśP2A1A2ŁŹĄśP3A2A3ŁŹĄŁŹĄśPnAn-1An¶ŒÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹĐ±±ßOA1ĄąA1A2ĄąA2A3ŁŹĄŁŹAn-1An¶ŒÔÚxÖáÉÏŁšnÊÇŽóÓÚ»ò”ÈÓÚ2”ÄŐęŐûÊ꣩ŁŹÈôĄśP1OA2”ÄÄÚœÓŐę·œĐÎB1C1D1E2”ÄÖÜł€ŒÇÎȘl1ŁŹĄśP2A1A2”ÄÄÚœÓŐę·œĐÎB2C2D2E2”ÄÖÜł€ŒÇÎȘl2ŁŹĄŁŹĄśPnAn-1An”ÄÄÚœÓŐę·œĐÎBnCnDnEn”ÄÖÜł€ŒÇÎȘlnŁŹÔòÓĂșŹn”ÄÊœŚÓ±íÊŸl1+l2+l3+Ą+lnÎȘŁšĄĄĄĄŁ©| AŁź | $\frac{8\sqrt{n}}{3}$ | BŁź | 2$\sqrt{n}$ | CŁź | $\frac{4\sqrt{n}}{3}$ | DŁź | $\frac{2\sqrt{n}}{3}$ |
·ÖÎö ÓÉÓÚĄśP1OA1ÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹżÉÖȘÖ±ÏßOP1”ÄœâÎöÊœÎȘy=xŁŹœ«ËüÓëy=$\frac{1}{x}$ŁšxŁŸ0Ł©ÁȘÁąŁŹÇółö·œłÌŚé”ÄœâŁŹ”Ă”œ”ăP1”ÄŚű±êŁŹÔòA1”ÄșáŚű±êÊÇP1”ÄșáŚű±ê”ÄÁœ±¶ŁŹŽÓ¶űÈ·¶š”ăA1”ÄŚű±êŁ»ÓÉÓÚĄśP1OA1ŁŹĄśP2A1A2¶ŒÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁŹÔòA1P2ĄÎOP1ŁŹÖ±ÏßA1P2żÉżŽŚśÊÇÖ±ÏßOP1ÏòÓÒÆœÒÆOA1žö”„λł€¶È”Ă”œ”ÄŁŹÒò¶ű”Ă”œÖ±ÏßA1P2”ÄœâÎöÊœŁŹÍŹŃùŁŹœ«ËüÓëy=$\frac{1}{x}$ŁšxŁŸ0Ł©ÁȘÁąŁŹÇółö·œłÌŚé”ÄœâŁŹ”Ă”œ”ăP2”ÄŚű±êŁŹÔòP2”ÄșáŚű±êÊÇÏ߶ÎA1A2”ÄÖД㣏ŽÓ¶űÈ·¶š”ăA2”ÄŚű±êŁ»ÒÀŽËÀàÍÆŁŹŽÓ¶űÈ·¶š”ăAn”ÄŚű±êŁŹ”ĂłöOAn”Äł€ŁŹÈ»șóžùŸĘl1=$\frac{4}{3}$OA1ŁŹl2=$\frac{4}{3}$A1A2ŁŹl3=$\frac{4}{3}$A2A3Ąln=$\frac{4}{3}$An-1AnŁŹŒŽżÉÇó”Ăl1+l2+l3+Ą+ln=$\frac{4}{3}$OAn=$\frac{4}{3}$ĄÁ2 $\sqrt{n}$=$\frac{8}{3}$$\sqrt{n}$Łź
œâŽđ œâŁșčęP1ŚśP1M1ĄÍxÖáÓÚM1ŁŹÈçÍŒËùŁș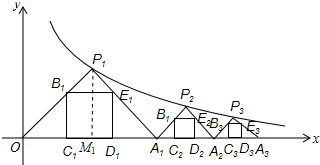
ÒŚÖȘM1Łš1ŁŹ0Ł©ÊÇOA1”ÄÖД㣏
ĄàA1Łš2ŁŹ0Ł©Łź
żÉ”ĂP1”ÄŚű±êÎȘŁš1ŁŹ1Ł©ŁŹ
ĄàP1O”ÄœâÎöÊœÎȘŁșy=xŁŹ
ĄßP1OĄÎA1P2ŁŹ
ĄàA1P2”ıíŽïʜһŽÎÏîÏ”ÊęÏà”ÈŁŹ
œ«A1Łš2ŁŹ0Ł©ŽúÈëy=x+bŁŹ
Ąàb=-2ŁŹ
ĄàA1P2”ıíŽïÊœÊÇy=x-2ŁŹ
Óëy=$\frac{1}{x}$ŁšxŁŸ0Ł©ÁȘÁąŁŹœâ”ĂP2Łš1+$\sqrt{2}$ŁŹ-1+$\sqrt{2}$Ł©Łź
·ÂÉÏŁŹA2Łš2$\sqrt{2}$ŁŹ0Ł©Łź
P3Łš$\sqrt{2}$+$\sqrt{3}$ŁŹ-$\sqrt{2}$+$\sqrt{3}$Ł©ŁŹA3Łš2$\sqrt{3}$ŁŹ0Ł©Łź
ÒÀŽËÀàÍÆŁŹ”ăAn”ÄŚű±êÎȘŁš2$\sqrt{n}$ŁŹ0Ł©ŁŹ
Ąßl1=$\frac{4}{3}$OA1ŁŹl2=$\frac{4}{3}$A1A2ŁŹl3=$\frac{4}{3}$A2A3Ąln=$\frac{4}{3}$An-1AnŁŹ
Ąàl1+l2+l3+Ą+ln=$\frac{4}{3}$OAn=$\frac{4}{3}$ĄÁ2$\sqrt{n}$=$\frac{8}{3}$$\sqrt{n}$Łź
čÊŃĄŁșAŁź
”ăÆÀ ±ŸÌâżŒČéÁË·Ž±ÈÀęșŻÊęÍŒÏóÉÏ”ă”ÄŚű±êÌŰŐśŁŹ”ÈŃüÖ±œÇÈęœÇĐΔÄĐÔÖÊŁŹŐę·œĐΔÄĐÔÖÊ”ÈŁŹčŰŒüÊÇŐÒłöÇóP”ăŚű±ê”ÄčæÂÉŁŹÒÔŐâžöčæÂÉÎȘ»ùŽĄÇółöPn”ÄșáŚű±êŁŹœű¶űÇółöAn”ÄșáŚű±ê”ÄÖ”ŁŹŽÓ¶űżÉ”ĂłöËùÇó”ÄœáčûŁź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | 0žö | BŁź | 1žö | CŁź | 2žö | DŁź | 3žö |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
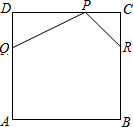 ÈçÍŒŁŹŐę·œĐÎABCDÊÇÒ»ŐƱ߳€ÎȘ12č«·Ö”ÄÆ€žïŁźÆ€”ńÊŠž”ÏëÔÚŽËÆ€žïÁœÏàÁڔĜÇÂä·Ö±đÇĐÏÂĄśPDQÓ륜PCRșó”Ă”œÒ»žöÎć±ßĐÎPQABRŁŹÆäÖĐPD=2DQŁŹPC=RCŁŹÇÒPĄąQĄą
ÈçÍŒŁŹŐę·œĐÎABCDÊÇÒ»ŐƱ߳€ÎȘ12č«·Ö”ÄÆ€žïŁźÆ€”ńÊŠž”ÏëÔÚŽËÆ€žïÁœÏàÁڔĜÇÂä·Ö±đÇĐÏÂĄśPDQÓ륜PCRșó”Ă”œÒ»žöÎć±ßĐÎPQABRŁŹÆäÖĐPD=2DQŁŹPC=RCŁŹÇÒPĄąQĄąČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
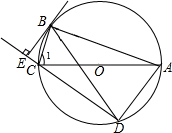 ÈçÍŒŁŹĄŃOÊÇĄśABC”ÄÍâœÓÔČŁŹACÎȘÖ±Ÿ¶ŁŹÏÒBD=BAŁŹBEĄÍDCœ»DC”ÄŃÓł€ÏßÓÚ”ăEŁź
ÈçÍŒŁŹĄŃOÊÇĄśABC”ÄÍâœÓÔČŁŹACÎȘÖ±Ÿ¶ŁŹÏÒBD=BAŁŹBEĄÍDCœ»DC”ÄŃÓł€ÏßÓÚ”ăEŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
 ÈçÍŒŁŹABĄÎCDŁŹAEœ»CDÓÚ”ăCŁŹDEĄÍAEÓÚ”ăEŁŹÈôĄÏA=42ĄăŁŹÔòĄÏD=48ĄăŁź
ÈçÍŒŁŹABĄÎCDŁŹAEœ»CDÓÚ”ăCŁŹDEĄÍAEÓÚ”ăEŁŹÈôĄÏA=42ĄăŁŹÔòĄÏD=48ĄăŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | ÖÚÊę | BŁź | ·œČî | CŁź | ÆœŸùÊę | DŁź | ÖĐλÊę |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | $\sqrt{18}$ | BŁź | $\sqrt{\frac{1}{3}}$ | CŁź | $\sqrt{24}$ | DŁź | $\sqrt{0.3}$ |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com