
分析 (1)只需利用三角函数就可解决问题;
(2)表示出RH,FC建立方程求解即可.
(3)可分△PQR全部在△ABC内和△PQR部分在△ABC内两种情况讨论:当△PQR全部在△ABC内时,只需运用三角形的面积公式就可解决问题;当△PQR部分在△ABC内时,只需运用割补法就可解决问题;
(4)可通过构造K型全等,并利用相似三角形的性质来解决问题.
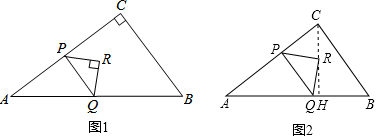
解答 解:(1)如图①,
由题意可知AP=4t,
tanA=$\frac{PQ}{AP}=\frac{BC}{AC}=\frac{3}{4}$,
∴PQ=3t;
(2)如图①,点R恰好落在BC上时,RH=PC=4-4t=$\frac{3}{2}$t,
∴t=$\frac{8}{11}$.
(3)①当0<t≤$\frac{8}{11}$时,如图①.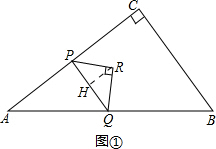
过点R作RH⊥PQ于点H,
S=$\frac{1}{2}$PQ•RH=$\frac{1}{2}$×3t×$\frac{3}{2}$t=$\frac{9}{4}$t2.
②当$\frac{8}{11}$<t<1时,如图③.
过点R作RH⊥PQ于点H,交BC于点G,
则有RG⊥MN,RH=$\frac{1}{2}$PQ=$\frac{3}{2}$t,GH=PC=4-4t,
∴S=S△RPQ-S△RMN=$\frac{1}{2}$PQ•RH-$\frac{1}{2}$MN•RH
=RH2-RG2=($\frac{3}{2}$t)2-[$\frac{3}{2}$t-(4-4t)]2
=-28t2+44t-16;
(4)点P在AC上,且点R在AB的高CH上,如图④,
过点P作PG⊥CH于G,
易证△PGR≌△RHQ,则有PG=RH,GR=QH.
易求得AB=5,CH=$\frac{12}{5}$,AH=$\frac{16}{5}$,BH=$\frac{9}{5}$.
PC=4-4t,CG=$\frac{3}{5}$PC=$\frac{3}{5}$(4-4t),PG=$\frac{4}{5}$PC=$\frac{4}{5}$(4-4t),
AQ=$\frac{4}{5}$AP=5t,QH=AH-AQ=$\frac{16}{5}$-5t.
根据CH=CG+GR+RH=CG+QH+PG=$\frac{12}{5}$,得
$\frac{3}{5}$(4-4t)+$\frac{16}{5}$-5t+$\frac{4}{5}$(4-4t)=$\frac{12}{5}$,
解得:t=$\frac{32}{53}$.
点评 此题是三角形综合题,主要考查了三角函数、等腰直角三角形的性质、直角三角形斜边上的中线等于斜边的一半、角平分线的性质、全等三角形的判定与性质、相似三角形的判定与性质等知识,在解决问题的过程中,用到了割补法和分类讨论等重要的数学思想方法,准确分类是解决本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ | C. | $\sqrt{6}$$÷\sqrt{2}$=$\sqrt{3}$ | D. | ($\sqrt{2}$+1)($\sqrt{2}$-1)=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com