Question

已知关于x的二次函数y=-x²+（2m+3）x+4-m²的图象与x轴交于A、B两点，点A在点B的左边，与y轴的交点C在原点的上方，若A、B两点到原点的距离AO、OB满足4（OB-AO）=3AO•OB．
（1）求这个二次函数的解析式；
（2）求这个二次函数图象的顶点M的坐标，并画出函数图象的略图；
（3）求△AMC的面积．

Answer 1

分析：（1）本题可根据韦达定理和题中给出的OA、OB的关系式来求m的值，以此来得出抛物线的解析式；
（2）根据（1）得出的抛物线的解析式可用配方法或公式法求出M的坐标；
（3）由于三角形ACM的面积无法直接求出，设AM与y轴的交点为D，可将其分割成三角形ADC和CDM两部分来求．可先求出直线AM的解析式，得出D的坐标后再求三角形AMC的面积．

解答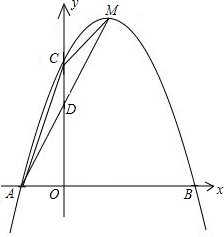：解：（1）∵抛物线与y轴的交点在原点上方，且抛物线开口向下
∴A、B必在原点两侧．
∵点A在点B的左边，因此A在x轴的负半轴，B在x轴的正半轴．
设A（x₁，0），B（x₂，0），那么OA=-x₁，OB=x₂．
则有：x₁+x₂=2m+3，x₁x₂=m²-4．
∵4（OB-AO）=3AO•OB，即4（x₂+x₁）=-3x₁x₂；
4（2m+3）=-3（m²-4），
解得m=0，m=-

8

3

，
∵抛物线与y轴的交点C在y轴正半轴
∴4-m²＞0，即-2＜m＜2，
∴m=0．
∴抛物线的解析式为y=-x²+3x+4；

（2）由（1）知：y=-x²+3x+4=-（x-

3

2

）²+

25

4

，
∴M（

3

2

，

25

4

）；

（3）设直线AM与y轴的交点为D．
易知A（-1，0），M（

3

2

，

25

4

），
∴直线AM的解析式为y=

5

2

x+

5

2

．
∴D（

5

2

，

5

2

），
∴CD=OC-OD=4-

5

2

=

3

2

，
∴S_△ACM=S_△ACD+S_△CDM=

1

2

×

3

2

×1+

1

2

×

3

2

×

3

2

=

15

8

．

点评：本题考查了二次函数与一元二次方程的关系、一元二次方程根与系数的关系、函数解析式的确定、图形面积的求法、函数图象交点等知识．