
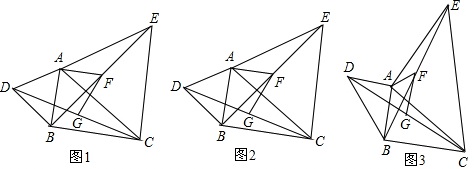
分析 (1)根据等式的性质就可以得出∠DAC=∠BAE.就可以得出△ADC≌△ABE就可以得出DG=BF;
(2)如图2,连接AG,根据全等三角形的性质得到CD=BE,∠ADC=∠ABE,由G、F分别是DC与BE的中点,得到DG=BF,推出△ADG≌△ABF,根据全等三角形的性质即可得到结论;
(3)连接AG,根据条件就可以得出△ADG≌△ABF,就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性质就可以求出∠AFG的值,;
(4)连接AG,根据条件就可以得出△ADG≌△ABF,就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性质就可以表示β与a的关系.
解答 解:(1)∵∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
∴∠DAC=∠BAE.
在△ADC和△ABE
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△ADC≌△ABE(SAS),
∴DC=BE,
∵G、F分别是DC与BE的中点,
∴DG=$\frac{1}{2}$CD,BF=$\frac{1}{2}$BE,
∴DG=BF;
故答案为:=;
(2)如图2,连接AG,
∵△ADC≌△ABE,
∴CD=BE,∠ADC=∠ABE,
∵G、F分别是DC与BE的中点,
∴DG=$\frac{1}{2}$CD,BF=$\frac{1}{2}$BE,
∴DG=BF,
在△ADG与△ABF中,$\left\{\begin{array}{l}{AD=AB}\\{∠ADG=∠ABF}\\{DG=BF}\end{array}\right.$,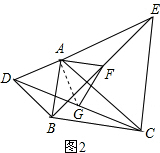
∴△ADG≌△ABF,
∴AG=AF,
∴△AFG是等腰三角形;
(3)如图3,连接AG.
∵△ADC≌△ABE,
∴∠ADC=∠ABE.AD=AB.
∵G、F分别是DC与BE的中点,
∴DG=$\frac{1}{2}$DC,BF=$\frac{1}{2}$BE,
∴DG=BF.
在△ADG和△ABF中
$\left\{\begin{array}{l}{AD=AB}\\{∠ADC=∠ABE}\\{DG=BF}\end{array}\right.$,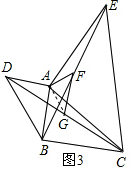
∴△ADG≌△ABF(SAS),
∴AG=AF,∠DAG=∠BAF,
∴∠AGF=∠AFG,∠DAG-∠BAG=∠BAF-∠BAG,
∴∠DAB=∠GAF.
∵∠DAB=100°,
∴∠GAF=100°.
∵∠GAF+∠AFG+∠AGF=180°,
∴∠AFG=40°;
故答案为:40°;
(4)∵∠DAB=a,
∴∠GAF=a.
∵∠GAF+∠AFG+∠AGF=180°,
∴a+2β=180°.
点评 本题考查了全等三角形的判定及性质的运用,等式的性质的运用,等腰三角形的性质的运用,三角形内角和定理的运用,解答时证明三角形全等是关键.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,A、B为公路l同旁的两个村庄,在l上找一点P.
如图所示,A、B为公路l同旁的两个村庄,在l上找一点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 由示意图可见,抛物线y=x2+px+q若有两点A(a,yl)、B(b,y2)(其中a<b)在x轴下方,则抛物线必与x轴有两个交点C(x1,O)、D(x2,O)(其中xl<x2),且满足xl<a<b<x2.当A(1,-2005),且xl、x2均为整数时,求二次函数的表达式.
由示意图可见,抛物线y=x2+px+q若有两点A(a,yl)、B(b,y2)(其中a<b)在x轴下方,则抛物线必与x轴有两个交点C(x1,O)、D(x2,O)(其中xl<x2),且满足xl<a<b<x2.当A(1,-2005),且xl、x2均为整数时,求二次函数的表达式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,则∠ACB等于( )| A. | ∠EDB | B. | $\frac{1}{2}$∠AFB | C. | ∠BED | D. | $\frac{1}{2}$∠ABF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com