
分析 (1)分两种情况讨论:①当k=0时,方程是一元一次方程,有实数根;②当k≠0时,方程是一元二次方程,所以证明判别式是非负数即可;
(2)先根据根与系数的关系表示出x1+x2,x1x2,再代入方程求关于k的方程即可.
解答 (1)证明:①当k=0时,x-2=0,得x=2,有实数根;
②当k≠0时,方程是一元二次方程,
∵△=(3k-1)2-4k×2(k-1)=(k+1)2≥0,
∴无论k为何实数,方程总有实数根;
综上所述,无论k为何实数,方程总有实数根;
(2)解:∵方程有两个实数根,
∴k≠0,方程为一元二次方程.
由已知可得x1+x2=$\frac{3k-1}{k}$,x1x2 =$\frac{2(k-1)}{k}$,
∵x1+x2-x1x2 =2,
∴$\frac{3k-1}{k}$-$\frac{2(k-1)}{k}$=2,
∴k=1.
点评 本题主要考查一元二次方程根的判别式和根与系数的关系的应用,同时考查了学生的综合应用能力及推理能力.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
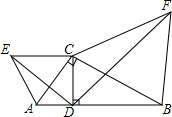 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,分别以AC,BC为边向三角形外作等边△ACE和等边△BCF,连接DE,DF,试说明:△ADE∽△CDF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:
设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14% | B. | 15% | C. | 16% | D. | 17% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com