
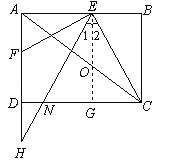
【题目】在矩形ABCD中,AB=4,BC=3,E是AB边上一点,EF⊥CE交AD于点F,过点E作∠AEH=∠BEC,交射线FD于点H,交射线CD于点N.
(1)如图a,当点H与点F重合时,求BE的长;
(2)如图b,当点H在线段FD上时,设BE=x,DN=y,求y与x之间的函数关系式,并写出它的定义域;
(3)连接AC,当△FHE与△AEC相似时,求线段DN的长.

【答案】(1)BE=3;(2)y=2x﹣4(2≤x≤3);(3)DN的长为![]() 或1.
或1.
【解析】
(1)由已知条件证明BE=BC即可求出BE的长;
(2)过点E作EG⊥CN,垂足为点G,利用矩形的性质和等腰三角形的性质证明CN=2CG=2BE,即可得到y与x之间的函数关系式;
(3)首先证明∠HFE=∠AEC,当△FHE与△AEC相似时,再分∠FHE=∠EAC和∠FHE=∠ECA两种情况求出满足题意的DN的值即可.
(1)∵EF⊥EC,
∴∠AEF+∠BEC=90°.
∵∠AEF=∠BEC,
∴∠AEF=∠BEC=45°.
∵∠B=90°,
∴BE=BC.
∵BC=3,
∴BE=3;
(2)过点E作EG⊥CN,垂足为点G,
∴四边形BEGC是矩形,
∴BE=CG.
∵AB∥CN,
∴∠AEH=∠ENC,∠BEC=∠ECN.
∵∠AEH=∠BEC,
∴∠ENC=∠ECN,
∴EN=EC,
∴CN=2CG=2BE.
∵BE=x,DN=y,CD=AB=4,
∴y=2x﹣4(2≤x≤3);
(3)∵∠BAD=90°,
∴∠AFE+∠AEF=90°.
∵EF⊥EC,
∴∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∴∠HFE=∠AEC,
当△FHE与△AEC相似时,分两种情况讨论:
①若∠FHE=∠EAC.
∵∠BAD=∠B,∠AEH=∠BEC,
∴∠FHE=∠ECB,
∴∠EAC=∠ECB,
∴tan∠EAC=tan∠ECB,
∴![]() .
.
∵AB=4,BC=3,
∴BE=![]() .
.
∵设BE=x,DN=y,y=2x﹣4,
∴DN=![]() ;
;
②若∠FHE=∠ECA,如所示,设EG与AC交于点O.
∵EN=EC,EG⊥CN,
∴∠1=∠2.
∵AH∥EG,
∴∠FHE=∠1,
∴∠FHE=∠2,
∴∠2=∠ECA,
∴EO=CO.
设EO=CO=3k,则AE=4k,AO=5k,
∴AO+CO=8k=5,
∴k=![]() ,
,
∴AE=![]() ,BE=
,BE=![]() ,
,
∴DN=1.
综上所述:线段DN的长为![]() 或1时,△FHE与△AEC相似.
或1时,△FHE与△AEC相似.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按拟定的价格进行试销,通过对5天的试销情况进行统计,得到如下数据:

(1)通过对上面表格中的数据进行分析,发现销量y(件)与单价![]() (元/件)之间存在一次函数关系,求y关于
(元/件)之间存在一次函数关系,求y关于![]() 的函数关系式(不需要写出函数自变量的取值范围);
的函数关系式(不需要写出函数自变量的取值范围);
(2)预计在今后的销售中,销量与单价仍然存在(2)中的关系,且该产品的成本是20元/件.为使工厂获得最大利润,该产品的单价应定为多少?
(3)为保证产品在实际试销中销售量不得低于30件,且工厂获得得利润不得低于400元,请直接写出单价![]() 的取值范围;
的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
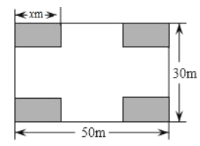
【题目】某社区决定把一块长![]() ,宽
,宽![]() 的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于
的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于![]() ,不大于
,不大于![]() ,设绿化区较长边为
,设绿化区较长边为![]() ,活动区的面积为
,活动区的面积为![]() .为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于
.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于![]() ,算出
,算出![]() .
.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/![]() ,绿化区造价为40元/
,绿化区造价为40元/![]() ,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
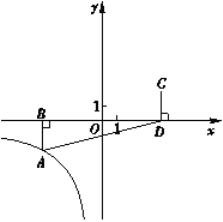
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王某承包了甲、乙两片荒山,各栽了100棵杨梅树,现已全部挂果,为了分析收成情况,他分别从两山上各采摘了4棵树上的全部杨梅,每棵树的产量如折线统计图.
(1)分别计算甲、乙两山样本的平均数,并估计出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
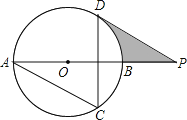
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
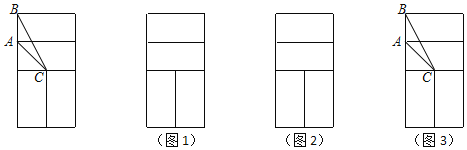
【题目】如图是四个全等的小矩形组成的图形,这些矩形的顶点称为格点.△ABC是格点三角形(顶点是格点的三角形)
(1)若每个小矩形的较短边长为1,则BC= ;
(2)①在图1、图2中分别画一个格点三角形(顶点是格点的三角形),使它们都与△ABC相似(但不全等),且图1,2中所画三角形也不全等).
②在图3中只用直尺(没有刻度)画出△ABC的重心M.(保留痕迹,点M用黑点表示,并注上字母M)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,求二次函数的表达式;
(2)在(1)的条件下,设二次函数的图象与y轴交于点C,且在同一平面内,以A,B,C,P为顶点的四边形为平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于代数式![]() ,下列说法正确的是( )
,下列说法正确的是( )
①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则![]() ;
;
②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c;
③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c;
④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c.
A.①B.③C.②④D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com