练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，以点O为位似中心，将△ABC放大得到△DEF，若AD=OA，则△ABC与△DEF的面积之比为 ．

    1：4. 【解析】 试题解析：∵以点O为位似中心，将△ABC放大得到△DEF，AD=OA， ∴AB：DE=OA：OD=1：2， ∴△ABC与△DEF的面积之比为：1：4．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第23章 旋转 单元测试卷 题型：填空题

    请写出一个是中心对称图形的几何图形的名称：　 　．

    平行四边形（答案不唯一）。 【解析】【解析】 平行四边形是中心对称图形． 故答案可为：平行四边形．

    查看答案和解析>>

    科目：初中数学 来源：安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型：解答题

    先将代数式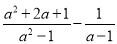进行化简，然后请你选择一个合适的值，并求代数式的值.

    ，当=2时，原式的值为2 【解析】试题分析：先根据分式成立的条件求出a的取值范围，再通分，把代数式化简后取一个合适的a值代入进行计算． 试题解析：原式= 当=2时， 原式. （注意： ≠±1）

    查看答案和解析>>

    科目：初中数学 来源：安徽省蚌埠市2017届九年级下学期中考二模数学试卷 题型：单选题

    已知点P(3,-2)与点Q关于x轴对称，则Q点的坐标为( )

    A. (-3,2) B. (-3,-2) C. (2,3) D. (3,2)

    D 【解析】试题解析：根据轴对称的性质，得点P（3，-2）关于x轴对称的点的坐标为（3，2）． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：解答题

    如图，在△ABC中，AB=AC，∠A=36°，BD为角平分线，DE⊥AB，垂足为E．

    （1）写出图中一对全等三角形和一对相似比不为1的相似三角形；

    （2）选择（1）中一对加以证明．

    （1）△ADE≌△BDE，△ABC∽△BCD；（2）证明见解析． 【解析】试题分析：（1）利用相似三角形的性质以及全等三角形的性质得出符合题意的答案； （2）利用相似三角形的判定以及全等三角形的判定方法分别得出即可． 试题解析：【解析】 （1）△ADE≌△BDE，△ABC∽△BCD； （2）证明：∵AB=AC，∠A=36°， ∴∠ABC=∠C=72°， ∵BD...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：单选题

    如图，铁路道口的栏杆短臂长1m，长臂长16m.当短臂端点下降0.5m时，长臂端点升高（杆的宽度忽略不计）

    A. 4m B. 6m C. 8m D. 12m

    C 【解析】试题分析：设长臂端点升高x米，则，∴解得：x=8．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：第二十七章 达标检测卷 题型：单选题

    若，则等于（　　）

    A. 8 B. 9 C. 10 D. 11

    C 【解析】试题解析：设， 则a=2k，b=3k，c=4k， 即， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年甘肃省武威市凉州区洪祥镇九年级（上）期末数学试卷 题型：单选题

    已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论有（　　）

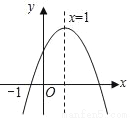
    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】试题分析：开口向下，则a＜0，对称轴在y轴右边，则b＞0，与y轴交于正半轴，则c＞0，∴abc＜0，∴①正确；当x=－1时，y＜0，即a－b+c＜0，∴b＞a+c，∴②正确；因为对称轴为1，即－=1，则 2a=－b，∴2a+b=0，∴③错误；∵图象与x轴有两个交点，则－4ac＞0，∴④错误．

    查看答案和解析>>

    科目：初中数学 来源：人教版九年级下册 期中测试卷 题型：填空题

    将三角形纸片（△ABC）按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．已知AB＝AC＝6，BC＝8．若以点B′，F，C为顶点的三角形与△ABC相似，则BF的长度是______

    4或． 【解析】设BF= ，则由折叠的性质可知：B′F= ，FC= ， （1）当△B′FC∽△ABC时，有， 即： ，解得： ； （2）当△B′FC∽△BAC时，有， 即： ，解得： ； 综上所述，可知：若以点B′，F，C为顶点的三角形与△ABC相似，则BF的长度是4或. 故答案为：4或.

    查看答案和解析>>

    同步练习册答案