
如图,直线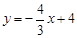 与
与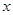 轴、
轴、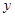 轴分别交于
轴分别交于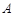 、
、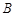 两点,△
两点,△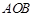 绕点
绕点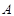 顺时针旋转90后得到△
顺时针旋转90后得到△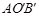 ,则点
,则点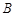 的对应点
的对应点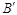 坐标为
坐标为

A.(3,4) B.(7,4)
C.(7,3) D.(3,7)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 与
与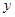 轴的交点坐标为A(0,1),与
轴的交点坐标为A(0,1),与 轴的交点坐标为B(-3,0);P、Q分别是
轴的交点坐标为B(-3,0);P、Q分别是 轴和直线AB上的一动
轴和直线AB上的一动
查看答案和解析>>
科目:初中数学 来源: 题型:
 S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;
S四边形OQPB时,请确定点P在AB上的位置,并求出线段PQ的长;
查看答案和解析>>
科目:初中数学 来源:2013届浙江临安於潜第一初级中学九年级上期末综合考试数学试卷(一)(带解析) 题型:解答题
(本题12分)
如图,直线 与
与 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥ 轴),并且分别与
轴),并且分别与 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江临安於潜第一初级中学九年级上期末综合考试数学试卷(一)(解析版) 题型:解答题
(本题12分)
如图,直线 与
与 轴、
轴、 轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从
轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动.
动直线EF从 轴开始以每秒1个长度单位的速度向上平行移动(即EF∥
轴开始以每秒1个长度单位的速度向上平行移动(即EF∥ 轴),并且分别与
轴),并且分别与 轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.
轴、线段AB交于E、F点.连结FP,设动点P与动直线EF同时出发,运动时间为t秒.

(1)当t=1秒时,求梯形OPFE的面积;
(2)t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3)设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(福建漳州卷)数学 题型:解答题
(11·漳州)(满分14分)如图1,抛物线y=mx2-11mx+24m (m<0) 与x轴交于B、C两点(点B在点C的左侧),抛物线另有一点A在第一象限内,且∠BAC=90°.
(1)填空:OB=_ ▲ ,OC=_ ▲ ;
(2)连接OA,将△OAC沿x轴翻折后得△ODC,当四边形OACD是菱形时,求此时抛物线的解析式;
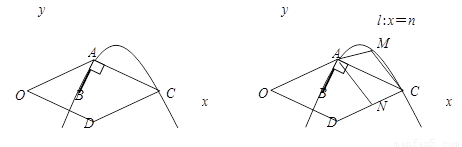 (3)如图2,设垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
(3)如图2,设垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com