
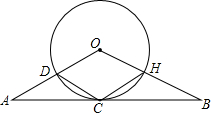
 如图,等腰三角形AOB的一边BC经过⊙O上的一点C,AO=BO,CA=CB,OA与⊙O交于点D,OB与⊙O交于点H,连接CD、CH.
如图,等腰三角形AOB的一边BC经过⊙O上的一点C,AO=BO,CA=CB,OA与⊙O交于点D,OB与⊙O交于点H,连接CD、CH.分析 (1)根据等腰三角形的三线合一可得OC⊥AB,则根据切线的判定定理可判断AB与⊙O相切;
(2)先根据等腰三角形的性质得OC平分∠AOB,即∠DOC=∠HOC,再证明△OCD≌△OCH,得到∠OCD=∠OCH,由于∠AOB=∠DCH,则∠DOC=∠OCD,所以DO=DC,则OD=OC=CD,同理可得CH=OH,所以OD=DC=CH=OH,由此可判断四边形ODCH为菱形.
解答  (1)证明:∵AO=BO,CA=CB,
(1)证明:∵AO=BO,CA=CB,
∴OC⊥AB,
∴AB与⊙O相切;
(2)解:四边形ODCH为菱形.理由如下:
∵AO=BO,CA=CB,
∴OC平分∠AOB,即∠DOC=∠HOC,
在△OCD和△OCH中,
$\left\{\begin{array}{l}{OD=OH}\\{∠DOC=∠HOC}\\{OC=OC}\end{array}\right.$,
∴△OCD≌△OCH,
∴∠OCD=∠OCH,
∵∠AOB=∠DCH,
∴∠DOC=∠OCD,
∴DO=DC,
∵OD=OC,
∴OD=OC=CD,
同理可得CH=OH,
∴OD=DC=CH=OH,
∴四边形ODCH为菱形.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了等腰三角形的判定与性质和菱形的判定.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$cm | B. | $\sqrt{3}$cm | C. | 3cm | D. | $\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 测量某天的最低气温,结果是-150℃ | |
| B. | 三角形内角和等于180° | |
| C. | 随意翻一本书的页码,这页的页码是奇数 | |
| D. | 通常加热到100℃时,水沸腾 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x3-x=x(x2-1) | B. | x2+y2=(x+y)(x-y) | C. | (a+4)(a-4)=a2-16 | D. | m2+m+$\frac{1}{4}$=(m+$\frac{1}{2}$)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).
如图,△ABC的3个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形,该图中与△ABC全等的不同格点三角形共有15个(△ABC除外).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com