
【题目】如图,矩形![]() 中,
中,![]() ,连接
,连接![]() ,以对角线
,以对角线![]() 为边按逆时针方向作矩形
为边按逆时针方向作矩形![]() ,使矩形
,使矩形![]() 矩形
矩形![]() ;再连接
;再连接![]() ,以对角线
,以对角线![]() 为边,按逆时针方向作矩形,使矩形
为边,按逆时针方向作矩形,使矩形![]() 矩形
矩形![]() , ..按照此规律作下去,若矩形
, ..按照此规律作下去,若矩形![]() 的面积记作
的面积记作![]() ,矩形
,矩形![]() 的面积记作
的面积记作![]() ,矩形
,矩形![]() 的面积记作
的面积记作![]() , ... 则
, ... 则![]() 的值为__________.
的值为__________.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】数学问题:用边长相等的正三角形、正方形和正六边形能否进行平面图形的镶嵌?
问题探究:为了解决上述数学问题,我们采用分类讨论的思想方法去进行探究.
探究一:从正三角形、正方形和正六边形中任选一种图形,能否进行平面图形的镶嵌?
第一类:选正三角形.因为正三角形的每一个内角是60°,所以在镶嵌平面时,围绕某一点有6个正三角形的内角可以拼成一个周角,所以用正三角形可以进行平面图形的镶嵌.
第二类:选正方形.因为正方形的每一个内角是90°,所以在镶嵌平面时,围绕某一点有4个正方形的内角可以拼成一个周角,所以用正方形也可以进行平面图形的镶嵌.
第三类:选正六边形.(仿照上述方法,写出探究过程及结论)
探究二:从正三角形、正方形和正六边形中任选两种图形,能否进行平面图形的镶嵌?
第四类:选正三角形和正方形
在镶嵌平面时,设围绕某一点有x个正三角形和y个正方形的内角可以拼成个周角.根据题意,可得方程
60x+90y=360
整理,得2x+3y=12.
我们可以找到唯一组适合方程的正整数解为![]() .
.
镶嵌平面时,在一个顶点周围围绕着3个正三角形和2个正方形的内角可以拼成一个周角,所以用正三角形和正方形可以进行平面镶嵌
第五类:选正三角形和正六边形.(仿照上述方法,写出探究过程及结论)
第六类:选正方形和正六边形,(不写探究过程,只写出结论)
探究三:用正三角形、正方形和正六边形三种图形是否可以镶嵌平面?
第七类:选正三角形、正方形和正六边形三种图形.(不写探究过程,只写结论),
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=![]() ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )

A. ![]() B. 3 C. 2 D. 2
B. 3 C. 2 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司引进A,B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题:

(1)求yB关于x的函数解析式;
(2)如果A,B两种机器人连续搬运5小时,那么B种机器人比A种机器人多搬运了多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
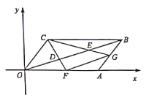
【题目】在平面直角坐标系中,平行四边形![]() 的顶点
的顶点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,点
,点![]() 把线段
把线段![]() 三等分,延长
三等分,延长![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() , 则下列结论:
, 则下列结论:![]() ;
; ![]()
![]() ③四边形
③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ,其中正确的有( ).
,其中正确的有( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义新知)在数轴上,点M和点N分别表示数x1和x2 ,可以用绝对值表示点M、N两点间的距离d (M,N),即d (M,N)=|x1-x2|.
(初步应用)
(1)在数轴上,点A、B、C分别表示数-1、2、x, 解答下列问题:
①d (A,B)= ;
②若d(A,C)=2,则x的值为 ;
③若d(A,C)+d(B,C)=d(A,B),且x为整数,则x的取值有 个.
(综合应用)
(2)在数轴上,点D、E、F分别表示数-2、4、6.动点P沿数轴从点D开始运动,到达F点后立刻返回,再回到D点时停止运动.在此过程中,点P的运动速度始终保持每秒2个单位长度.设点P的运动时间为t秒.
①当t= 时,d(D,P)=3;
②在整个运动过程中,请用含t的代数式表示d(E,P).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形纸片![]() ,其中
,其中![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 上的点,连接
上的点,连接![]() .
.
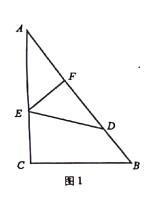
(1)如图1,若将纸片![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 刚好落在
刚好落在![]() 边上点
边上点![]() 处,且
处,且![]() ,求
,求![]() 的长;
的长;
(2)如图2,若将纸片![]() 沿
沿![]() 折叠,折叠后点
折叠,折叠后点![]() 刚好落在
刚好落在![]() 边上点
边上点![]() 处,且
处,且![]() .
.
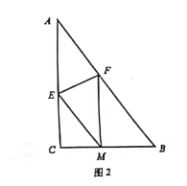
![]() 试判断四边形
试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 求折痕
求折痕![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )
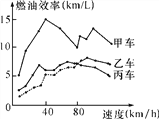
A. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
B. 以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
C. 以高于80 km/h的速度行驶时,行驶相同路程,丙车比乙车省油
D. 以80 km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①②③是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.

(1)图①中△MON的面积=________;
(2)在图②③中以格点为顶点画出一个正方形ABCD,使正方形ABCD的面积等于(1)中△MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD的面积没有剩余(在图②、图③中画出的图形不能是全等形)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com