
分析 (1)根据有理数的加法和减法可以解答本题;
(2)根据有理数的乘法和除法可以解答本题;
(3)根据有理数的乘法、加法和减法可以解答本题;
(4)根据有理数的加法和减法可以解答本题.
解答 解:(1)(-5.2)-(+4.8)+3.2
=(-5.2)+(-4.8)+3.2
=(-10)+3.2
=-6.8;
(2)-2$\frac{1}{3}$×(-1$\frac{1}{6}$)÷(-7)×$\frac{1}{7}$
=$-\frac{7}{3}×(-\frac{7}{6})×(-\frac{1}{7})×\frac{1}{7}$
=-$\frac{1}{18}$;
(3)23-6×(-3)+2×(-4)
=23-(-18)+(-8)
=23+18+(-8)
=33;
(4)(-0.5)-(-3$\frac{1}{4}$)+2.75-(-7$\frac{1}{2}$)
=(-0.5)+$3\frac{1}{4}$+2.75+$7\frac{1}{2}$
=13.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,MN分 别交OA、OB于E、F.
如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,MN分 别交OA、OB于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
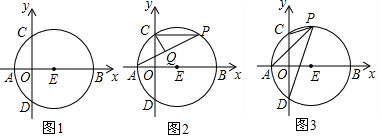
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,P是$\widehat{EF}$上的一点,若∠A=70°,求∠BOC、∠EPF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,P是$\widehat{EF}$上的一点,若∠A=70°,求∠BOC、∠EPF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等边△ABC的边长为6,折叠△ABC,使得点A恰好与边BC上的点D重合,折痕为EF(点E、F分别在边AB、AC上)
如图,已知等边△ABC的边长为6,折叠△ABC,使得点A恰好与边BC上的点D重合,折痕为EF(点E、F分别在边AB、AC上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com