Question

1．在平面直角坐标系中，点A（0，b）、点B（a，0）、点D（d，0）且a、b、c满足$\sqrt{a+1}$+$\sqrt{b-3}$+（2-d）²=0，DE⊥x轴且∠BED=∠ABD，BE交y轴于点C，AE交x轴于点F．
（1）求点A、B、D的坐标；
（2）求点E、F的坐标；
（3）如图，过P（0，-1）作x轴的平行线，在该平行线上有一点Q（点Q在P的右侧）使∠QEM=45°，QE交x轴于N，ME交y轴正半轴于M，求$\frac{AM-MQ}{PQ}$的值．

Answer 1

分析 （1）由非负数的性质可求得a、b、d的值，可求得A、B、D的坐标；
（2）由条件可证明△ABO≌△BED，可求得DE和BD的长，可求得E点坐标，再求得直线AE的解析式，可求得F点坐标；
（3）过E作EG⊥OA于点G，EH⊥PQ于点Q，可证明四边形GEHP为正方形，在GA上截GI=QH，可证明△IGE≌△QHE，可证得∠IEM=∠MEQ=45°，可证明△EIM≌△EQM，可得到IM=MQ，再结合条件可求得PH=AI=PQ，可求得答案．

解答 解：（1）∵$\sqrt{a+1}$+$\sqrt{b-3}$+（2-d）²=0，
∴a=-1，b=3，d=2，
∴A（0，3），B（-1，0），D（2，0）；
（2）∵A（0，3），B（-1，0），D（2，0），
∴OB=1，OD=2，OA=3，
∴AO=BD，
在△ABO和△BED中，
$\left\{\begin{array}{l}{∠ABO=∠BED}\\{∠AOB=∠BDE=90°}\\{AO=BD}\end{array}\right.$，
∴△ABO≌△BED（AAS），
∴DE=BO=1，
∴E（2，1），
设直线AE解析式为y=kx+b，如图1，

把A、E坐标代入可得$\left\{\begin{array}{l}{3=b}\\{1=2k+b}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$，
∴直线AE的解析式为y=-x+3，
令y=0，可解得x=3，
∴F（3，0）；
（3）过E作EG⊥OA，EH⊥PQ，垂足分别为G、H，在GA上截取GI=QH，如图2，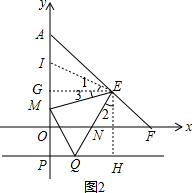

∵E（2，1），P（-1，0），
∴GE=GP=GE=PH=2，
∴四边形GEHP为正方形，
∴∠IGE=∠EHQ=90°，
在Rt△IGE和Rt△QHE中，
$\left\{\begin{array}{l}{GE=HE}\\{∠IGE=∠EHQ}\\{IG=QH}\end{array}\right.$
∴△IGE≌△QHE（SAS），
∴IE=EQ，∠1=∠2，
∵∠QEM=45°，
∴∠2+∠3=45°，
∴∠1+∠3=45°，
∴∠IEM=∠QEM，
在△EIM和△EQM中，
$\left\{\begin{array}{l}{IE=QE}\\{∠IEM=∠QEM}\\{ME=ME}\end{array}\right.$，
∴△EIM=EQM（SAS），
∴IM=MQ，
∴AM-MQ=AM-IM=AI，
由（2）可知OA=OF=3，∠AOF=90°，
∴∠A=∠AEG=45°，
∴PH=GE=GA=IG+AI，
∴AI=GA-IG=PH-QH=PQ，
∴$\frac{AM-MQ}{PQ}$=$\frac{AI}{PQ}$=1．

点评 本题主要考查一次函数的综合应用，涉及知识点有非负数的性质、全等三角形的判定和性质、待定系数法、正方形的判定和性质知．在（1）中掌握非负数的性质是解题的关键，在（2）中证明△ABO≌△BED求得DE的长是解题的关键，在（3）中构造三角形全等证明AM-MQ=AI=PQ是解题的关键．本题涉及知识点较多，综合性较强，难度较大，特别是第（3）问中条件∠QEM=45°角的应用是解题的关键点．