
分析 (1)先利用对称轴公式x=-$\frac{b}{2a}$计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
(2)根据三角形的三边关系:可知P、C、D三点共线时|PC-PD|取得最大值,求出直线CD与x轴的交点坐标,就是此时点P的坐标;
(3)先把函数中的绝对值化去,可知y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3(x≥0)}\\{-{x}^{2}-2x+3(x<0)}\end{array}\right.$,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2-2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(-3,0),即点P与点(-3,0)重合时,线段PQ与当函数y=a|x|2-2a|x|+c(x<0)时也有一个公共点,则当t≤-3时,都满足条件;综合以上结论,得出t的取值.
解答 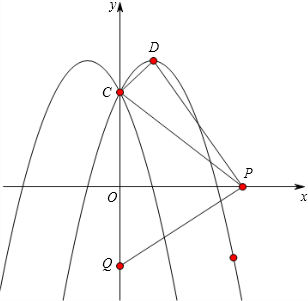 解:(1)∵y=ax2-2ax+c的对称轴为:x=-$\frac{-2a}{2a}$=1,
解:(1)∵y=ax2-2ax+c的对称轴为:x=-$\frac{-2a}{2a}$=1,
∴抛物线过(1,4)和($\frac{7}{2}$,-$\frac{9}{4}$)两点,
代入解析式得:$\left\{\begin{array}{l}{a-2a+c=4}\\{\frac{49}{4}a-7a+c=-\frac{9}{4}}\end{array}\right.$,
解得:a=-1,c=3,
∴二次函数的解析式为:y=-x2+2x+3,
∴顶点D的坐标为(1,4);
(2)∵C、D两点的坐标为(0,3)、(1,4);
由三角形两边之差小于第三边可知:
|PC-PD|≤|CD|,
∴P、C、D三点共线时|PC-PD|取得最大值,此时最大值为,
|CD|=$\sqrt{2}$,
由于CD所在的直线解析式为y=x+3,
将P(t,0)代入得t=-3,
∴此时对应的点P为(-3,0);
(3)y=a|x|2-2a|x|+c的解析式可化为:
y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3(x≥0)}\\{-{x}^{2}-2x+3(x<0)}\end{array}\right.$,
设线段PQ所在的直线解析式为y=kx+b,将P(t,0),Q(0,2t)代入得:
线段PQ所在的直线解析式:y=-2x+2t,
∴①当线段PQ过点(0,3),即点Q与点C重合时,线段PQ与函数
y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3(x≥0)}\\{-{x}^{2}-2x+3(x<0)}\end{array}\right.$有一个公共点,此时t=$\frac{3}{2}$,
当线段PQ过点(3,0),即点P与点(3,0)重合时,t=3,此时线段PQ与
y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3(x≥0)}\\{-{x}^{2}-2x+3(x<0)}\end{array}\right.$有两个公共点,所以当$\frac{3}{2}$≤t<3时,
线段PQ与y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3(x≥0)}\\{-{x}^{2}-2x+3(x<0)}\end{array}\right.$有一个公共点,
②将y=-2x+2t代入y=-x2+2x+3(x≥0)得:
-x2+2x+3=-2x+2t,
-x2+4x+3-2t=0,
令△=16-4(-1)(3-2t)=0,
t=$\frac{7}{2}$>0,
所以当t=$\frac{7}{2}$时,线段PQ与y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3(x≥0)}\\{-{x}^{2}-2x+3(x<0)}\end{array}\right.$也有一个公共点,
③当线段PQ过点(-3,0),即点P与点(-3,0)重合时,线段PQ只与
y=-x2-2x+3(x<0)有一个公共点,此时t=-3,
所以当t≤-3时,线段PQ与y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3(x≥0)}\\{-{x}^{2}-2x+3(x<0)}\end{array}\right.$也有一个公共点,
综上所述,t的取值是$\frac{3}{2}$≤t<3或t=$\frac{7}{2}$或t≤-3.
点评 本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
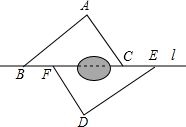 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y-$\frac{1}{y}$-3=0 | B. | y-$\frac{4}{y}$-3=0 | C. | y-$\frac{1}{y}$+3=0 | D. | y-$\frac{4}{y}$+3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
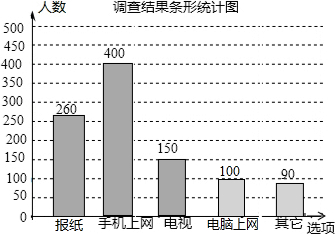 如图是某市电视台记者为了解市民获取新闻的主要图径,通过抽样调查绘制的一个条形统计图.若该市约有230万人,则可估计其中将报纸和手机上网作为获取新闻的主要途径的总人数大约为151.8万人.
如图是某市电视台记者为了解市民获取新闻的主要图径,通过抽样调查绘制的一个条形统计图.若该市约有230万人,则可估计其中将报纸和手机上网作为获取新闻的主要途径的总人数大约为151.8万人.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为122°.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为122°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com