
【题目】万州苏宁电器某品牌洗衣机销售情况良好,2018年11月份初该洗衣机每台的进价为2280元,购进了600台该品牌洗衣机.
(1)如果该商场为了减小库存压力,想把购进的600台该品牌洗衣机在11月底全部销售完,商场决定利用打折来促销,每台洗衣机在标价的基础上打8折,这样很快销售一空.要使该商场获得利润不低于72000元,则每台洗衣机的标价应不低于多少元?
(2)该商场决定12月初继续购进600台该品牌洗衣机销售,据悉,2018年12月份因全国经济出现通货膨胀,商品价格进一步上涨,商场决定该品牌洗衣机的销售价格比(1)中的最低标价上涨m%,但实际销售量比11月份下降了![]() m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
【答案】(1)每台洗衣机的标价应不低于3000元;(2)m的值为0.25
【解析】
(1)设每台洗衣机的标价应为x元,根据题意列出不等式即可求出x的范围;
(2)11月份的最低标价为3000元,11月份的销售额为3000×600=1800000,12月份的销售价格为:3000+3000×m%,12月份的销售量为:600-600×![]() m%,根据题意列出方程即可求出答案.
m%,根据题意列出方程即可求出答案.
解:(1)设每台洗衣机的标价应为x元,
根据题意可知:600(0.8x﹣2280)≥72000,
解得:x≥3000,
答:每台洗衣机的标价应不低于3000元;
(2)11月份的最低标价为3000元,
11月份的销售额为3000×600=1800000,
12月份的销售价格为:3000+3000×m%,
12月份的销售量为:600﹣600×![]() m%,
m%,
∴(3000+3000×m%)(600﹣600×![]() m%)=1800000,
m%)=1800000,
∴解得:m%=0(舍去)或m%=![]() ,
,
∴m=25,
答:m的值为25.


科目:初中数学 来源: 题型:
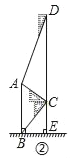
【题目】腾飞中学在教学楼前新建了一座“腾飞”雕塑(如图①).为了测量雕塑的高度,小明利用三角板测得雕塑顶端A点的仰角为30°,底部B点的俯角为45°,小华在五楼找到一点D,利用三角板测得A点的俯角为60°(如图②).若已知CD为10米,请求出雕塑AB的高度.(结果精确到0.1米,参考数据![]() =1.73).
=1.73).

查看答案和解析>>
科目:初中数学 来源: 题型:
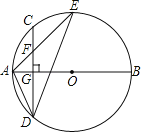
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;④S△DEF=4
;④S△DEF=4![]() .
.
其中正确的是 (写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
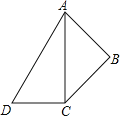
【题目】如图所示,将一副三角板摆放在一起,组成四边形ABCD,∠ABC=∠ACD=90°,∠ADC=60°,∠ACB=45°,连接BD,则tan∠CBD的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以一个等腰直角三角形的腰为边分别向形外做等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”.如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学要利用长为24m的篱笆围成一个长方形花圃,形状如图,一边靠墙(墙的最大可用长度为9m),中间隔有一道篱笆,设AB长为x米,围成的花圃面积为S平方米.
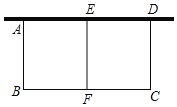
(1)求S关于x的函数解析式;并写出自变量x的取值范围.
(2)当AB多长时,围成的花圃有最大面积?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣1)2+4的图象经过点(﹣1,0).
(1)求这个二次函数的解析式;
(2)判断这个二次函数的开口方向,对称轴和顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com