
【题目】为构建“魅力雨花,和谐雨花,人文雨花”,规划在圭塘河上修建一座观光人行桥(如图1),此工程由桥梁工程与桥上拱形工程组成,桥上拱形工程包含三组完全相同的拱形,观光人行桥的正规图如图2所示,已知桥面上三组拱桥都为相同的抛物线![]() 的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.
的一部分,拱高(抛物线最高点到桥面的距离)为16米,三条抛物线依次与桥面AB相较于点A,C,D,B.

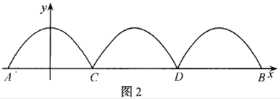
(1)求桥长AB;
(2)已知一组桥拱的造价为a万元,桥面每米的平均造价为b万元.若一组桥拱的造价为整个桥面造价的![]() ,这座观光桥的总造价为504万元,求a,b的值.
,这座观光桥的总造价为504万元,求a,b的值.
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]()
![]() 经过
经过![]() ,
,![]() 两点,点
两点,点![]() 为抛物线的顶点,抛物线的对称轴与
为抛物线的顶点,抛物线的对称轴与![]() 轴交于点
轴交于点![]() .
.

(1)求抛物线的解析式;
(2)动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 向终点
向终点![]() 作匀速运动,速度为每秒1个单位长度,运动时间为
作匀速运动,速度为每秒1个单位长度,运动时间为![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,以
,以![]() 为正方形的一边,向上作正方形
为正方形的一边,向上作正方形![]() ,边
,边![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
①当![]() 为何值时,点
为何值时,点![]() 落在抛物线上;
落在抛物线上;
②在点![]() 运动过程中,是否存在某一时刻,使得四边形
运动过程中,是否存在某一时刻,使得四边形![]() 为平行四边形?若存在,求出此时刻的
为平行四边形?若存在,求出此时刻的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴上方抛物线上一点,点
轴上方抛物线上一点,点![]() 是直线
是直线![]() 上一点,若
上一点,若![]() 以为顶点的四边形是以
以为顶点的四边形是以 ![]() 为边的平行四边形,求点
为边的平行四边形,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣2ax﹣3a分别交x轴于A、B两点(点A在点B的侧),与y轴交于点C,连接AC,tan∠ACO=![]() .
.
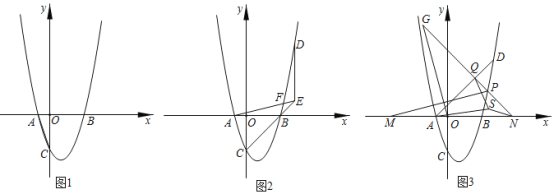
(1)如图l,求a的值;
(2)如图2,D是第一象限抛物线上的点,过点D作y轴的平行线交CB的延长线于点E,连接AE交BD于点F,AE=BD,求点D的坐标;
(3)如图3,在(2)的条件下,连接AD,P是第一象限抛物线上的点(点P与点D不重合),过点P作AD的垂线,垂足为Q,交x轴于点N,点M在x轴上(点M在点N的左侧),点G在NP的延长线上,MP=OG,∠MPN﹣∠MOG=45°,MN=10![]() .点S是△AQN内一点,连接AS、QS、NS,AS=AQ,QS=
.点S是△AQN内一点,连接AS、QS、NS,AS=AQ,QS=![]() SN,求QS的长.
SN,求QS的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过B(3,0),C(0,-3)两点,点D为顶点.
经过B(3,0),C(0,-3)两点,点D为顶点.
(1)求抛物线的解析式及顶点D的坐标;
(2)点E在抛物线的对称轴上,F在BD上,求BE+EF的最小值;
(3)点P是抛物线第四象限的点(不与B、C重合),连接PB,以PB为边作正方形BPMN,当点M或N恰好落在对称轴上时,求出对应的P点的坐标(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
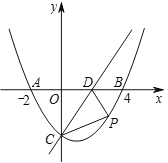
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的解析式.
(2)点![]() 是抛物线上第四象限上的一个动点,连接
是抛物线上第四象限上的一个动点,连接![]() ,
,![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标.
的坐标.
(3)将抛物线的对称轴向左平移3个长度单位得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若直线
,若直线![]() 上存在使
上存在使![]() 最大的点
最大的点![]() ,请直接写出满足条件的点
,请直接写出满足条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法正确的是( )
A.小明做了![]() 次掷图钉的实验,发现
次掷图钉的实验,发现![]() 次钉尖朝上,由此他说钉尖朝上的概率是
次钉尖朝上,由此他说钉尖朝上的概率是![]()
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.点![]() 都在反比例函数
都在反比例函数![]() 图象上,且
图象上,且![]() 则
则![]() ;
;
D.对于一元二元方程![]() ,若
,若![]() 则方程的两个根互为相反数
则方程的两个根互为相反数
查看答案和解析>>
科目:初中数学 来源: 题型:
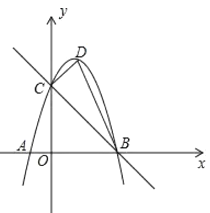
【题目】如图,以![]() 为顶点的抛物线
为顶点的抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 的表达式为
的表达式为![]() .
.
(1)求抛物线的表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上有一点
上有一点![]() ,若使
,若使![]() 的值最小,则点
的值最小,则点![]() 的坐标为____________.
的坐标为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com