解:(1)∵将抛物线y=-x
2平移,平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),
∴平移后的抛物线的表达式为y=-(x+1)(x-3)=-x
2+2x+3,即y=-x
2+2x+3,
∵y=-x
2+2x+3=-(x-1)
2+4,
∴顶点D的坐标为(1,4);
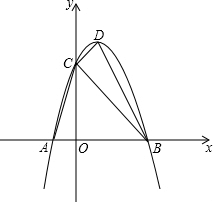
(2)∠ACB与∠ABD相等,理由如下:
如图,∵y=-x
2+2x+3,
∴点x=0时,y=3,即C点坐标为(0,3),
又∵B(3,0),∠BOC=90°,
∴OB=OC,∠OBC=∠OCB=45°.
在△BCD中,∵BC
2=3
2+3
2=18,CD
2=1
2+1
2=2,BD
2=2
2+4
2=20,
∴BC
2+CD
2=BD
2,
∴∠BCD=90°,
∴tan∠CBD=

=
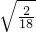
=

,
∵在△AOC中,∠AOC=90°,
∴tan∠ACO=
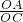
=

,
∴tan∠ACO=tan∠CBD,
∴∠ACO=∠CBD,
∴∠ACO+∠OCB=∠CBD+∠OBC,
即∠ACB=∠ABD;
(3)∵点P在平移后的抛物线的对称轴上,而y=-x
2+2x+3的对称轴为x=1,
∴可设P点的坐标为(1,n).
∵△ABC是锐角三角形,
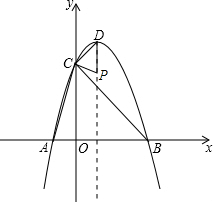
∴当△CDP与△ABC相似时,△CDP也是锐角三角形,
∴n<4,即点P只能在点D的下方,
又∵∠CDP=∠ABC=45°,
∴D与B是对应点,分两种情况:
①如果△CDP∽△ABC,那么

=
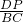
,
即

=
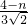
,
解得n=

,
∴P点的坐标为(1,

);
②如果△CDP∽△CBA,那么

=
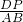
,
即
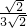
=
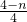
,
解得n=

,
∴P点的坐标为(1,

).
综上可知P点的坐标为(1,

)或(1,

).
分析:(1)根据平移不改变二次项系数a的值,且平移后的抛物线与x轴交于点A(-1,0)和点B(3,0),可知平移后抛物线的表达式为y=-(x+1)(x-3)=-x
2+2x+3,再运用配方法化为顶点式,即可求出顶点D的坐标;
(2)先由B、C两点的坐标,得出∠OBC=∠OCB=45°,再根据勾股定理的逆定理判断△BCD是直角三角形,且∠BCD=90°,则由正切函数的定义求出tan∠CBD=

,在△AOC中,由正切函数的定义也求出tan∠ACO=

,得出∠ACO=∠CBD,则∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD;
(3)设P点的坐标为(1,n),先由相似三角形的形状相同,得出△CDP是锐角三角形,则n<4,再根据∠CDP=∠ABC=45°,得到D与B是对应点,所以分两种情况进行讨论:①△CDP∽△ABC;
②△CDP∽△CBA.根据相似三角形对应边的比相等列出关于n的方程,解方程即可.
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的平移规律,对称轴、顶点坐标的求法,勾股定理及其逆定理,锐角三角函数的定义,相似三角形的判定与性质,综合性较强,难度适中.两个三角形相似没有明确对应顶点时要注意分析题意分情况讨论结果.

 抛物线y=-x2平移后的位置如图所示,点A,B坐标分别为(-1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D.
抛物线y=-x2平移后的位置如图所示,点A,B坐标分别为(-1,0)、(3,0),设平移后的抛物线与y轴交于点C,其顶点为D. (2)∠ACB与∠ABD相等,理由如下:
(2)∠ACB与∠ABD相等,理由如下: =
=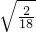 =
= ,
,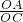 =
= ,
, ∴当△CDP与△ABC相似时,△CDP也是锐角三角形,
∴当△CDP与△ABC相似时,△CDP也是锐角三角形, =
=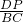 ,
, =
=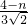 ,
, ,
, );
); =
=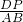 ,
,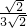 =
=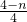 ,
, ,
, ).
). )或(1,
)或(1, ).
). ,在△AOC中,由正切函数的定义也求出tan∠ACO=
,在△AOC中,由正切函数的定义也求出tan∠ACO= ,得出∠ACO=∠CBD,则∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD;
,得出∠ACO=∠CBD,则∠ACO+∠OCB=∠CBD+∠OBC,即∠ACB=∠ABD;

 考前必练系列答案
考前必练系列答案