
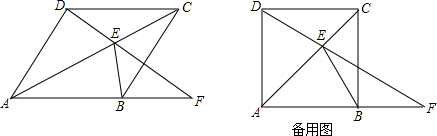
分析 (1)直接利用全等三角形的判定方法得出△DCE≌△BCE(SAS),即可得出答案;
(2)利用正方形的性质结合等腰三角形的性质得出:①当F在AB延长线上时;②当F在线段AB上时;分别求出即可.
解答 (1)证明:∵四边形ABCD是菱形,
∴CD=AB,∠ACD=∠ACB,
在△DCE和△BCE中
$\left\{\begin{array}{l}{DC=CB}\\{∠DCE=∠BCE}\\{EC=EC}\end{array}\right.$,
∴△DCE≌△BCE(SAS),
∴∠CDE=∠CBE,
∵CD∥AB,
∴∠CDE=∠AFD,
∴∠EBC=∠AFD;
(2)分两种情况:
①如图1,当F在AB延长线上时,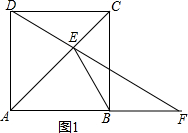
∵∠EBF为钝角,
∴只能是BE=BF,设∠BEF=∠BFE=x°,
可通过三角形内角形为180°得:90+x+x+x=180,
解得:x=30,
∴∠EFB=30°;
②如图2,当F在线段AB上时,
∵∠EFB为钝角,
∴只能是FE=FB,设∠BEF=∠EBF=x°,则有∠AFD=2x°,
可证得:∠AFD=∠FDC=∠CBE,
得x+2x=90,
解得:x=30,
∴∠EFB=120°.
综上:∠EFB=30°或120°.
点评 此题主要考查了菱形的性质以及正方形的性质以及全等三角形的判定与性质等知识,利用分类讨论得出是解题关键.


科目:初中数学 来源: 题型:解答题
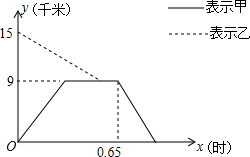 乙骑摩托车与B城相距15千米的A城办事,为了节省时间,甲同时从A城开车出发,先到达C城的D处,并在C城用了12分钟加油回到D处,此时乙已经到达D处等候甲3分钟了,乙把摩托车放到D处,乘甲开的汽车去A城,他们与A城的距离y千米与时间x之间的关系如图,回答下列问题:
乙骑摩托车与B城相距15千米的A城办事,为了节省时间,甲同时从A城开车出发,先到达C城的D处,并在C城用了12分钟加油回到D处,此时乙已经到达D处等候甲3分钟了,乙把摩托车放到D处,乘甲开的汽车去A城,他们与A城的距离y千米与时间x之间的关系如图,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
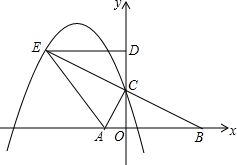 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
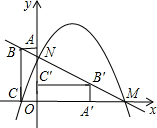 如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题:
如图,平面直角坐标系中,矩形OABC的顶点A(0,3),C(-1,0).将矩形OABC绕原点顺时针旋转90°,得到矩形OA′B′C′.解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com