
【题目】平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(a![]() ,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
(1)求点P(﹣2,3)的“2关联点”P′的坐标;
(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,6),求出k及点P的坐标;
(3)如图,点Q的坐标为(0,4![]() ),点A在函数y=﹣
),点A在函数y=﹣![]() (x<0)的图象上运动,且点A是点B的“﹣
(x<0)的图象上运动,且点A是点B的“﹣![]() 关联点”,当线段BQ最短时,求B点坐标.
关联点”,当线段BQ最短时,求B点坐标.
【答案】(1)P′(﹣![]() ,﹣1);(2)k=2,P′(1,4)、(2,2);(3)B(
,﹣1);(2)k=2,P′(1,4)、(2,2);(3)B(![]() ,
,![]()
![]() ).
).
【解析】
试题分析:(1)根据题中的新定义求出点P(﹣2,3)的“2关联点”P′的坐标即可;
(2)根据题中的新定义求出a与b的关系式即可;
(3)根据题意得出A(a﹣![]() ,﹣
,﹣![]() a+b),代入y=﹣
a+b),代入y=﹣![]() (x<0),求得b=
(x<0),求得b=![]() a+2
a+2![]() ,从而求得B在直线y=
,从而求得B在直线y=![]() x+2
x+2![]() 上,过Q作y=
上,过Q作y=![]() x+2
x+2![]() 的垂线QB1,垂足为B1,Q(0,4
的垂线QB1,垂足为B1,Q(0,4![]() ),且线段BQ最短,B1即为所求的B点,由△MB1Q∽△MON 得
),且线段BQ最短,B1即为所求的B点,由△MB1Q∽△MON 得![]() =
=![]() =
=![]() ,由ON=2,OM=2
,由ON=2,OM=2![]() ,根据勾股定理求得MN=4.由MQ=2
,根据勾股定理求得MN=4.由MQ=2![]() ,求得B1Q=
,求得B1Q=![]() ,MB1=3,在Rt△MB1Q中,根据面积公式得到B1QMB1=MQhB1,即可求得B的坐标.
,MB1=3,在Rt△MB1Q中,根据面积公式得到B1QMB1=MQhB1,即可求得B的坐标.
解:(1)∵x=﹣2+![]() =﹣
=﹣![]() ,y=2×(﹣2)+3=﹣1,
,y=2×(﹣2)+3=﹣1,
∴P′(﹣![]() ,﹣1);
,﹣1);
(2)设P(a,b),则P′(a+![]() ,ka+b)
,ka+b)
∴ ,
,
∴k=2,
∴2a+b=6.
∵a、b为正整数
∴P′(1,4)、(2,2);
(3)∵B的“﹣![]() 关联点”是A,
关联点”是A,
∴A(a﹣![]() ,﹣
,﹣![]() a+b),
a+b),
∵点A还在反比例函数y=﹣![]() 的图象上,
的图象上,
∴(﹣![]() a+b)(a﹣
a+b)(a﹣![]() )=﹣4
)=﹣4![]() ,
,
∴(b﹣![]() a)2=12,
a)2=12,
∵b﹣![]() a>0,
a>0,
∴b﹣![]() a=2
a=2![]() ,
,
∴b=![]() a+2
a+2![]() ;
;
∴B在直线y=![]() x+2
x+2![]() 上.
上.
过Q作y=![]() x+2
x+2![]() 的垂线QB1,垂足为B1,
的垂线QB1,垂足为B1,
∵Q(0,4![]() ),且线段BQ最短,
),且线段BQ最短,
∴B1即为所求的B点,
由△MB1Q∽△MON 得![]() =
=![]() =
=![]() ,
,
∵ON=2,OM=2![]() ,
,
∴MN=4.
又∵MQ=2![]() ,
,
∴B1Q=![]() ,MB1=3
,MB1=3
在Rt△MB1Q中,B1QMB1=MQhB1,
∴hB1=![]() ,
,
∴xB1=![]() ,
,
∴B(![]() ,
,![]()
![]() ).
).



 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
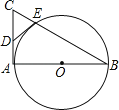
(1)若D为AC的中点,证明DE是⊙O的切线;
(2)若OA=![]() ,CE=1,求△ABC的面积.
,CE=1,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要招聘1名英语翻译,张明参加招聘考试的成绩如表所示:
听 | 说 | 读 | 写 | |
张明 | 90 | 80 | 83 | 82 |
若把听、说、读、写的成绩按3:3:2:2计算平均成绩,则张明的平均成绩为( )
A.82 B.83 C.84 D.85
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一粒大米的质量约为0.0000021千克,这个数用科学记数法表示为( )
A. 0.21×10-5 B. 2.1×10-5
C. 2.1×10-6 D. 21×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形一腰上的高与另一腰的夹角为50°,则该三角形的顶角的度数为( )
A. 40° B. 50° C. 40°或140° D. 50°或140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由二次函数y=2(x﹣3)2+1可知( )
A.其图象的开口向下
B.其图象的对称轴为x=﹣3
C.其最大值为1
D.当x<3时,y随x的增大而减小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com