
��ƽ��ֱ������ϵ��, ������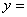
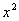 +
+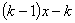 ��ֱ��
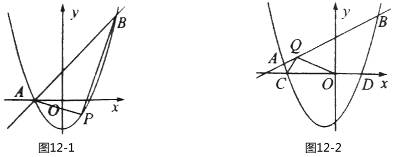
��ֱ��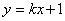 ����A, B���㣬��A�ڵ�B�����.
����A, B���㣬��A�ڵ�B�����.
(1) ��ͼ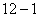 ����
���� ʱ��ֱ��д��A��B��������ꣻ
ʱ��ֱ��д��A��B��������ꣻ
(2) ��(1)�������£���PΪ�������ϵ�һ�����㣬����ֱ��AB�·����������ABP��������ֵ����ʱ��P�����ꣻ
(3) ��ͼ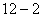 ��������
��������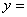
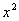 +
+ 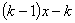
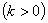 ��
�� �ύ��C��D���㣨��C�ڵ�D����ࣩ.��ֱ��
�ύ��C��D���㣨��C�ڵ�D����ࣩ.��ֱ��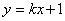 ���Ƿ����Ψһһ��Q��ʹ�á�OQC=90�㣿�����ڣ��������ʱ
���Ƿ����Ψһһ��Q��ʹ�á�OQC=90�㣿�����ڣ��������ʱ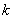 ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.


��1��A(-1,0) ��B(2,3)
���������д����k=1ʱ����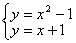 ����ɵ�
����ɵ�
��2��ƽ��ֱ��AB�õ�ֱ��L����L��������ֻ��һ������ʱ����ABP��������ͼ12-1��1����
��ֱ��L����ʽΪ��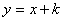 ��
��
����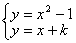 ����
����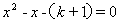
�б�ʽ��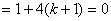 ����ã�
����ã�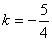
����ԭ�����У��� ����ã�
����ã�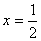 ��
�� 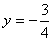
��P��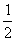 ,
,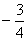 ��
��
����AB��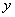 ����M��0��1����ֱ��L����
����M��0��1����ֱ��L����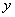 ��G��0��
��G��0��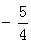 ��
��
��M��MN��ֱ��L��N����OM=1��OA=1�����AMO=45��
�ߡ�AMN=90�����NMO=45��
��RT��MNE�У���NMO=45�㣬MG=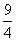 ������ͼ12-1��2����
������ͼ12-1��2����
�� MN= ��MN��Ϊ��ABP�ĸ�
��MN��Ϊ��ABP�ĸ�
���������빫ʽ����ã�AB=
�ʡ�ABP������

��3������ֱ��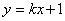 �ϴ���Ψһһ��Qʹ�á�OQC=90��
�ϴ���Ψһһ��Qʹ�á�OQC=90��
���QΪ��OC���е�EΪԲ�ģ�OCΪֱ���γɵ�ԲE��ֱ��
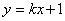 ����ʱ���е㡾��ͼ12-2��1����
����ʱ���е㡾��ͼ12-2��1����
�ɽ���ʽ��֪��C��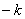 ,0����OC=
,0����OC=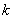 ����ԲE�İ뾶��OE=CE=
����ԲE�İ뾶��OE=CE=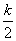 =QE
=QE
��ֱ��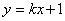 ��
�� ��
��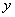 �ύ��H���F�㣬�룬
�ύ��H���F�㣬�룬
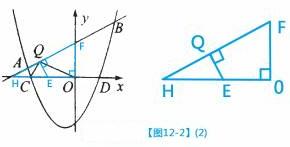 ��F��0,1������OF=1 ��H��
��F��0,1������OF=1 ��H��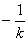 ,0���� ��OH =
,0���� ��OH =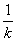
�� EH=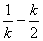
��AB���� ��EQ��AB����EQH=90��
�ڡ�FOH�͡�EQH�� 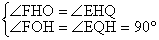
���FOH�ס�EQH
�� �� 1��
�� 1��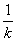 =
=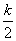 ��QH����QH =
��QH����QH =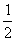
��RT��EQH��EH=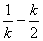 ��QH =
��QH =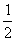 ��QE =
��QE =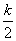 �����ݹ��ɶ����ã�
�����ݹ��ɶ����ã�
 +
+ =
=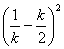
���





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
������Ϊ2cm����Ϊ1cm�ij����Σ��ڷ���ֱ��l�ϣ���ͼ�٣���CE=2cm����������ABCD���ŵ�C˳ʱ����ת���ǣ���������EFGH���ŵ�E��ʱ����ת��ͬ�ĽǶȣ�

��1������ת������D��H�غ�ʱ������AE��CG����֤����AED�ա�GCD����ͼ�ڣ���
��2������=45��ʱ����ͼ�ۣ�����֤���ı���MHNDΪ�����Σ�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ8����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4��.
(1) �뻭����ABC����ƽ��5����λ���Ⱥ�õ��ġ�A B
B C
C ��
��
(2) �뻭����ABC����ԭ��ԳƵġ�A B
B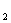 C
C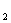 ��
��
(3) �� ��������һ��P��ʹ��PAB���ܳ���С���뻭����PAB����ֱ��д��P������.
��������һ��P��ʹ��PAB���ܳ���С���뻭����PAB����ֱ��д��P������.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�Ƕ��κ���y=ax2+bx+c��a��0��ͼ���һ���֣�x=��1�ǶԳ��ᣬ�������жϣ�
��b��2a=0����4a��2b+c��0����a��b+c=��9a����������3��y1������ ��y2���������������㣬��y1��y2��
��y2���������������㣬��y1��y2��
������ȷ���ǣ�������
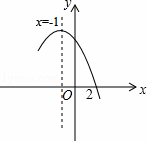
| �� | A�� | �٢ڢ� | B�� | �٢ۢ� | C�� | �٢ڢ� | D�� | �ڢۢ� |


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
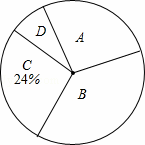
ijУ������ȤС���ڱ�Уѧ���п�չ���ж��й�2013�������Ƚ��¼�֪�����ר���������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����ΪA��B��C��D���࣮���У�A���ʾ���dz��˽⡱��B���ʾ���Ƚ��˽⡱��C���ʾ�������˽⡱��D���ʾ����̫�˽⡱����������������������±���
��� A B C D
Ƶ�� 30 40 24 b
Ƶ�� a 0.4 0.24 0.06
��1�����е�a=��0.3����b=��6����
��2�����ݱ������ݣ�������ͳ��ͼ�����ΪB��ѧ��������Ӧ������Բ�ĽǵĶ�����
��3������У��ѧ��1000�������ݵ��������Ƹ�Уѧ�������ΪC������ԼΪ���٣�


�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com