
1.从不同角度计算图中边长为c的正方形的面积,你得到了什么?发现了什么?与勾股定理有关吗?试试看.
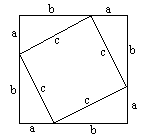
2.观察勾股定理a2+b2=c2中的c2、a2和b2,你想到了什么?
3.利用上图中四个完全相同的直角三角形,你还能拼出与c2有关的图形吗?能利用这个图形验证勾股定理吗?
4.用上图中的四个完全相同的直角三角形可以拼成如图Ⅰ所示的图形,这个图形被称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的.观察图Ⅰ,你能验证c2=a2+b2吗?把你的验证过程写下来,并与同伴进行交流.

2002年世界数学家大会(ICM-2002)在北京召开.图Ⅱ是此届大会的会标,其中央图案正是经过艺术处理的“弦图”.它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎来自世界各地的数学家们.

科目:初中数学 来源: 题型:

| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江宁波地八年级第一次质量评估数学试卷(带解析) 题型:解答题
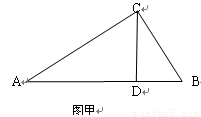
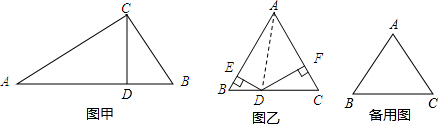
利用“等积”计算或说理是一种很巧妙的方法, 就是一个面积从两个不同的角度表示。如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长。
解题思路:利用勾股定理易得AB=5利用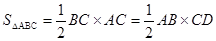 ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。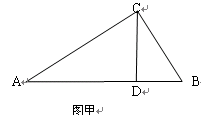
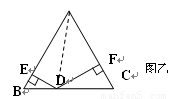
(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的
任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值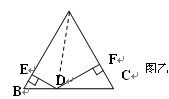
查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江宁波地八年级第一次质量评估数学试卷(解析版) 题型:解答题
利用“等积”计算或说理是一种很巧妙的方法, 就是一个面积从两个不同的角度表示。如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长。
解题思路:利用勾股定理易得AB=5利用
 ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。
(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的
任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
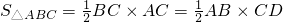 ,可得到CD=2.4
,可得到CD=2.4查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com