
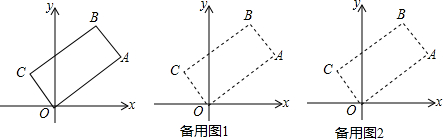
分析 (1)如图1所示:连接AC、OB,过点C作CE⊥x轴,AD⊥x轴.先证明△COE∽△OAD.由相似三角形的性质可求得CE=3,OE=4,从而可求得点C的坐标,接下来由矩形的性质可证明点F为AC、OB的中点,最后依据中点坐标公式可求得点B的坐标;
(2)当PQ=CQ时,过点Q作QD⊥CP,垂足为D.由等腰三角形三线合一的性质可求得CD=2,然后再证明四边形CDQO为矩形,从而可求得AQ的长,最后依据速度=路程÷时间求得k的值;当CP=CQ时,可求得OQ+OA=11,最后依据速度=路程÷时间求得k的值;
(3)如图4所示:当0≤t≤4时.由tan∠FOO′=$\frac{6}{8}$=$\frac{3}{4}$.可求得FO′=$\frac{5}{4}$t,最后依据三角形的面积公式可求得S与t的函数关系式;如图5所示:当4≤t≤6时.过点C′作C′E∥DO.由tan∠C′EO′=$\frac{3}{4}$,O′C′=5,可求得C′D=OE=$\frac{5}{3}$t-$\frac{20}{3}$.最后依据梯形的面积公式可求得S与t的函数关系式.
解答 解:(1)如图1所示:连接AC、OB,过点C作CE⊥x轴,AD⊥x轴.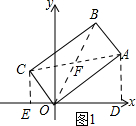
∵A(8,6),
∴AD=6,OD=8.
∵CE⊥x轴,AD⊥x轴,
∴∠CEO=∠ADO.
∵ABCO为矩形,
∴∠COA=90°,
∴∠COE+∠AOD=90°.
∵∠COE+∠OCE=90°,
∴∠OCE=∠AOD.
∴△COE∽△OAD.
∴$\frac{CE}{OD}=\frac{OE}{AD}=\frac{OC}{OA}=\frac{1}{2}$,即$\frac{CE}{6}=\frac{OE}{8}=\frac{1}{2}$.
∴CE=3,OE=4.
∴C(-3,4).
∵ABCO为矩形,
∴F为AC、OB的中点.
设点B的坐标为(x,y).则$\frac{x+0}{2}=\frac{-3+8}{2}$,$\frac{y+0}{2}=\frac{4+6}{2}$,解得:x=5,y=10.
∴点B的坐标为(5,10).
故答案为:C(-3,4);B(5,10).
(2)∵由两点间的距离公式可知:OA=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴OC=$\frac{1}{2}$OA=5.
∵PC=4,
∴PQ>PC.
如图2所示:当PQ=CQ时,过点Q作QD⊥CP,垂足为D.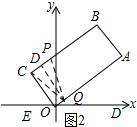
∵PQ=CQ,QD⊥CP,
∴CD=DP=2.
∵∠OCD=∠COQ=∠QDC=90°,
∴四边形CDQO为矩形.
∴OQ=CD=2.
∴AQ=10-2=8.
∴k=$\frac{8}{2}$=4.
如图3所示:当CP=CQ时,OQ+OA=10+1=11.
则k=$\frac{11}{2}$.
综上所述,当k=4或k=$\frac{11}{2}$时,△CQP为等腰三角形.
(3)如图4所示:当0≤t≤4时.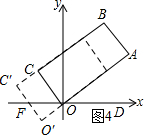
∵∠FOO′=∠AOD,
∴tan∠FOO′=$\frac{6}{8}$=$\frac{3}{4}$.
又∵OO′=$\frac{5}{3}$t,
∴FO′=$\frac{5}{4}$t.
∴S=$\frac{1}{2}$OF•O′F=$\frac{1}{2}$×$\frac{5}{4}$t•$\frac{5}{3}$t=$\frac{25}{24}$t2.
如图5所示:当4≤t≤6时.过点C′作C′E∥DO.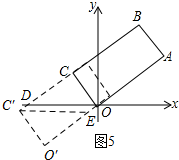
∵tan∠C′EO′=$\frac{3}{4}$,O′C′=5,
∴O′E=$\frac{20}{3}$.
∴C′D=OE=$\frac{5}{3}$t-$\frac{20}{3}$.
∴S=$\frac{1}{2}$O′C′(C′D+O′E)=$\frac{1}{2}$×5×[2×($\frac{5}{3}$t-$\frac{20}{3}$)+$\frac{20}{3}$]=$\frac{25t}{3}$-$\frac{50}{3}$.
综上所述,S与t的关系式为S=$\left\{\begin{array}{l}{\frac{25}{24}{t}^{2}(0≤t≤4)}\\{\frac{25}{3}t-\frac{50}{3}(4≤t≤6)}\end{array}\right.$.
点评 本题主要考查的是四边形、三角形的综合应用,解答本题主要应用了矩形的性质和判定、相似三角形的性质和判定、锐角三角函数的定义,分类讨论是解答问题(2)的关键,依据锐角三角函数的定义求得OO′、O′F、C′D的长度(用含t的式子表示)是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )
如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )| A. | 边边边 | B. | 角边角 | C. | 边角边 | D. | 角角边 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 看图填空:
看图填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 交通方式 | 频数(人数) | 频率 |
| 公共汽车 | m | 0.25 |
| 小车 | 24 | 0.20 |
| 摩托车 | 36 | n |
| 自行车 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图矩形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).
如图矩形ABCD中,点E在BC上,且AE=EC,试分别在下列两个图中按要求使用无刻度的直尺画图(保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a3+6ab2-5a2 | B. | a3-6ab2-5a2 | C. | a3-5a2 | D. | a2+6ab-5a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com