
����Ŀ����ͼ���ھ���![]() �У���
�У���![]() Ϊ����ԭ�㣬��
Ϊ����ԭ�㣬��![]() ����
����![]() ��
��![]() ���������ϣ���
���������ϣ���![]() ��
��![]() ���ϣ�ֱ��
���ϣ�ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() .��������ƽ���ڵ�ֱ�ߣ��Ƚ���ֱ������ƽ��
.��������ƽ���ڵ�ֱ�ߣ��Ƚ���ֱ������ƽ��![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ��![]() ����λ���ȣ�����ֱ���˶���Ϊֱ�ߵ�бƽ��.�ֽ�ֱ��
����λ���ȣ�����ֱ���˶���Ϊֱ�ߵ�бƽ��.�ֽ�ֱ��![]() ����
����![]() ��бƽ�ƣ��õ�ֱ��
��бƽ�ƣ��õ�ֱ��![]() .
.


������ͼ��
��1����ֱ��![]() ����������Χ�ɵ������
����������Χ�ɵ������
��2����ֱ��![]() ��
��![]() �Ľ������ꣻ
�Ľ������ꣻ
��3���ڵ�һ�����ڣ���ֱ��![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() �ǵ���ֱ�������Σ������ڣ���ֱ��д����
�ǵ���ֱ�������Σ������ڣ���ֱ��д����![]() �����꣬�������ڣ���˵������.
�����꣬�������ڣ���˵������.
���𰸡���1��![]() ����2��ֱ��
����2��ֱ��![]() ��
��![]() �Ľ�������
�Ľ�������![]() ����3�����ڵ�
����3�����ڵ�![]() �����꣺
�����꣺![]() ��
��![]() ��
��![]() .
.
��������
1��ֱ��![]() ����������Χ�ɵ����
����������Χ�ɵ����![]() ��������⣻
��������⣻
��2����ֱ��![]() ����2��бƽ�ƣ��õ�ֱ��
����2��бƽ�ƣ��õ�ֱ��![]() ��������⣻
��������⣻
��3����![]() Ϊֱ�ǡ�
Ϊֱ�ǡ�![]() Ϊֱ�ǡ�
Ϊֱ�ǡ�![]() Ϊֱ������������ɵ���ֱ�������ι���K����ȫ�ȣ������꽨�����̷ֱ���⼴�ɣ�
Ϊֱ������������ɵ���ֱ�������ι���K����ȫ�ȣ������꽨�����̷ֱ���⼴�ɣ�
�⣺��1��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��
![]() ֱ��
ֱ��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
![]() ��
��![]() ����
����![]() ����
����
![]() �����
�����![]() ��
��
![]() ֱ��
ֱ��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
��2��![]() ��ֱ��
��ֱ��![]() ����
����![]() ��бƽ�ƣ��õ�ֱ��
��бƽ�ƣ��õ�ֱ��![]()
![]() ֱ��
ֱ��![]()
![]() ֱ��
ֱ��![]()
��![]() ��
��![]()
��ֱ��![]() ��
��![]() �Ľ�������
�Ľ�������![]() ��
��
��3���ٵ�![]() Ϊֱ��ʱ����ͼ1��ʾ���ڵ�һ�����ڣ���ֱ��
Ϊֱ��ʱ����ͼ1��ʾ���ڵ�һ�����ڣ���ֱ��![]() �ϲ����ڵ�
�ϲ����ڵ�![]() ��
��
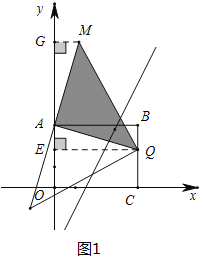
�ڵ�![]() Ϊֱ��ʱ��
Ϊֱ��ʱ��![]() ��
��
����![]() ��
��![]() ���ƽ���߷ֱ�
���ƽ���߷ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ����ͼ��3��
����ͼ��3��
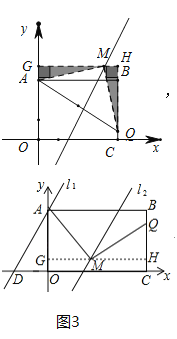 ��
��
���![]() ����
����![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]() ������
������![]() ��
��
��ã�![]() ��
��![]() ��
��
�ʵ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�۵�![]() Ϊֱ��ʱ����ͼ4��ʾ��
Ϊֱ��ʱ����ͼ4��ʾ��
 ��
��
��Q����FQ��ֱ��y�ᴹ��ΪF����M����MG��ֱFQ����ΪG��
ͬ���ɵã�FQ=MG��AF=DG��
��Q��������4��n����0��n��3����AF=DG=3-n��FQ=MG=4
��M��������7-n��4+n����
����![]() ����
����![]() ��
��
��ã�![]()
�ʵ�![]() ��
��
������������![]() �����꣺
�����꣺![]() ��
��![]() ��
��![]()


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD��BC��DC��BC���������ضԽ���BD�۵�����Aǡ������DC���ϵĵ�A����������A��BC��20�������A��BD�Ķ���Ϊ_____����
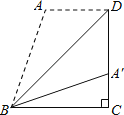
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ۿ�Pλ�ڶ�������ĺ������ϣ���Զ�����š������������ִ�ͬʱ�뿪�ۿڣ�������һ�̶������У���Զ������ÿСʱ����16�������������ÿСʱ����12��������뿪�ۿ�һ����Сʱ�ֱ�λ�ڵ�Q��R���������30������֪����Զ�������ر�ƫ��![]() �����У���������������ŵĺ��з���
�����У���������������ŵĺ��з���
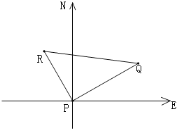
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵȱ�������ABC�У�CDΪ���ߣ���Q���߶�CD���˶������߶�QA�Ƶ�Q˳ʱ����ת��ʹ�õ�A�Ķ�Ӧ��E��������BC�ϣ�����BQ�����DAQ=��
��0�㣼����60��������30�㣩.
��1����0�㣼����30��ʱ��
����ͼ1�������⻭��ͼ�Σ������BQE���ú�����ʽ�ӱ�ʾ����
��̽���߶�CE��AC��CQ֮���������ϵ��������֤����
��2����30�㣼����60��ʱ��ֱ��д���߶�CE��AC��CQ֮���������ϵ.


![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��ֱ��
��ֱ��![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ��
��
��1����![]() ��ȵĽ���_____________��
��ȵĽ���_____________��
��2����![]() ����Ľ���______________��
����Ľ���______________��
��3����֪![]() ����
����![]() �Ķ�����
�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
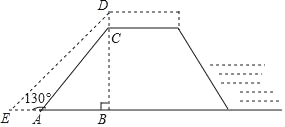
����Ŀ��Ϊ���÷�Ѵ��������Ѵָ�Ӳ�������ijˮ���ˮ�ӽ��мӸӹ̣�ר���ṩ�ķ����ǣ�ˮ�ӼӸ�2�ף���CD=2�ף�����ˮ��DE���¶�i=1��1����DB��EB=1��1������ͼ��ʾ����֪AE=4�ף���EAC=130������ˮ��ԭ���ĸ߶�BC�����ο����ݣ�sin50���0.77��cos50���0.64��tan50���1.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ�
�ϣ�![]() .����
.����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊһ����
Ϊһ����![]() �����ȱ�
�����ȱ�![]() ����
����![]() ��
��![]() Χ�ɵ����������ߣ��ڵ�һ�㣬����
Χ�ɵ����������ߣ��ڵ�һ�㣬����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() .��
.��![]() ��
��![]() ����
����![]() ���ֵ��_______.
���ֵ��_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����
A. �����콵��ĸ�����80%����ʾ������80%��ʱ�䶼�ڽ���
B. ����һöӲ�����泯�ϵĸ���Ϊ![]() ����ʾÿ��2�ξ���һ�����泯��
����ʾÿ��2�ξ���һ�����泯��
C. ����Ʊ�н��ĸ���Ϊ1%����ʾ��100�Ų�Ʊ�϶����н�
D. ����һö���������ӣ����ϵĵ���Ϊ2�ĸ���Ϊ![]() ����ʾ�����������������ӣ����׳����ϵĵ���Ϊ2����һ�¼�������Ƶ���ȶ���
����ʾ�����������������ӣ����׳����ϵĵ���Ϊ2����һ�¼�������Ƶ���ȶ���![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ����Ϊ4a����Ϊb�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ�����Ŀ�С������ƴ�ɵ�һ�������Ρ������Σ���ͼ2����
��ͼ2�е���Ӱ���ֵ����Ϊ ��
�ڹ۲�ͼ2����д�� ��a+b��2����a��b��2��ab֮��ĵ�����ϵ�� ��
�۸��ݣ�2���еĽ��ۣ���x+y=5��xy=![]() ����x��y��2= ��
����x��y��2= ��
��ʵ����ͨ������ͼ�ε��������̽����Ӧ�ĵ�ʽ��
��ͼ3���㷢�ֵĵ�ʽ�� ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com