
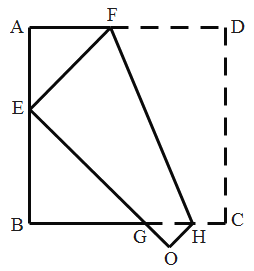
【题目】如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求△EBG的周长是__________cm.
【答案】12
【解析】
根据翻折变换的性质可得EF=FD,设AF=x,表示出EF,根据线段中点的定义求出AE=BE=3,再利用勾股定理列方程求出AF,然后求出△AEF和△BGE相似,根据相似三角形对应边成比例列式计算即可得解.
解:∵正方形ABCD折叠点D落在AB边的中点E处,
∴EF=FD,
设AF=x,则EF=6-x,
∵点E是AB的中点,
∴AE=BE=![]() ×6=3,
×6=3,
在Rt△AEF中,由勾股定理得,AE2+AF2=EF2,
即32+x2=(6-x)2,
解得x=![]() ,
,
∵∠FEG=90°,
∴∠AEF+∠BEG=90°,
∵∠BEG+∠BGE=90°,
∴∠AEF=∠BGE,
又∵∠A=∠B=90°,
∴△AEF∽△BGE,
∴![]() ,
,
∴BG=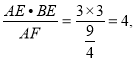
EG=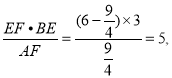
∴△EBG的周长=4+5+3=12.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
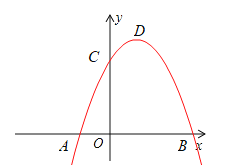
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为点
,顶点为点![]() .
.
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;(用含有
的坐标为 ;(用含有![]() 的代数式表示)
的代数式表示)
(2)连接![]() .
.
①若![]() 平分
平分![]() ,求二次函数的表达式;
,求二次函数的表达式;
②连接![]() ,若
,若![]() 平分
平分![]() ,求二次函数的表达式.
,求二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=![]() (x>0)和y=
(x>0)和y=![]() (x<0)的图象分别交于点P,Q.
(x<0)的图象分别交于点P,Q.
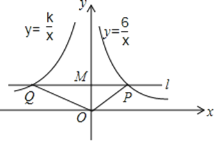
(1)求P点的坐标;
(2)若△POQ的面积为9,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防“流感”,某学校在休息日用“药熏”消毒法对教室进行消毒.已知药物释放过程中,室内每立方米的含药量y(毫克)与时间x(时)成正比例;药物释放结束后,y与x成反比例;如图所示,根据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与x之间的两个函数解析式;
(2)据测定,当药物释放结束后,每立方米的含药量降至0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多长时间,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增强学生的环保意识.随机抽取8名学生,对他们的垃圾分类投放情况进行调查,这8名学生分别标记为![]() ,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
,其中“√”表示投放正确,“×”表示投放错误,统计情况如下表.
学生 垃圾类别 |
|
|
|
|
|
|
|
|
厨余垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
可回收垃圾 | √ | × | √ | × | × | √ | √ | √ |
有害垃圾 | × | √ | × | √ | √ | × | × | √ |
其他垃圾 | × | √ | √ | × | × | √ | √ | √ |
(1)求8名学生中至少有三类垃圾投放正确的概率;
(2)为进一步了解垃圾分类投放情况,现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访,试用标记的字母列举所有可能抽取的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三信超市销售一种成本为每千克40元的水产品据市场分析,按每千克50元销告,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每干克55元时,求月销售利润;
(2)要使得月销售利润达到8000元又要薄利多销,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在地面上竖直安装着AB、CD、EF三根立柱,在同一时刻同一光源下立柱AB、CD形成的影子为BG与DH.

(1)填空:判断此光源下形成的投影是: 投影.
(2)作出立柱EF在此光源下所形成的影子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,N为边AD上一点,连接BN.过点A作AP⊥BN于点P,连接CP,M为边AB上一点,连接PM,∠PMA=∠PCB,连接CM,有以下结论:①△PAM∽△PBC;②PM⊥PC;③M、P、C、B四点共圆;④AN=AM.其中正确的个数为( )
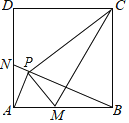
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com