
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形![]() 的边长是1米;
的边长是1米;
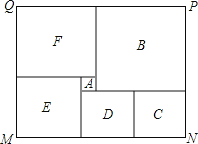
(1)若设图中最大正方形![]() 的边长是
的边长是![]() 米,请用含
米,请用含![]() 的代数式分别表示出正方形
的代数式分别表示出正方形![]() 的边长
的边长
(2)观察图形的特点可知,长方形相对的两边是相等的(即![]() ,
, ![]() )请根据以上结论,求出
)请根据以上结论,求出![]() 的值
的值
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要10天、15天完成,如果两队从同一位置开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,还要多少天完成?
【答案】(1)F的边长为(x-1)米;C的边长为![]() 米;E的边长为(x-2)米;(2)7;(3)10
米;E的边长为(x-2)米;(2)7;(3)10
【解析】
(1)若设图中最大正方形B的边长是x米,最小的正方形的边长是1米,从图中可看出F的边长为(x-1)米,C的边长为![]() ,E的边长为(x-1-1),即可得到答案;
,E的边长为(x-1-1),即可得到答案;
(2)根据长方形相对的两边是相等的(如图中的MN和P Q).请根据这个等量关系,求出x的值;
(3)根据工作效率×工作时间=工作量这个等量关系且完成工作,工作量就为1,可列方程求解.
解:(1)若设图中最大正方形B的边长是x米,最小的正方形的边长是1米.
∴F的边长为:(x-1)米,
∴C的边长为:![]() 米,
米,
∴E的边长为:x-1-1=(x-2)米;
(2)∵MQ=PN,
∴x-1+x-2=x+![]() ,
,
解得:x=7,
∴x的值为7;
(3)设余下的工程由乙队单独施工,还要x天完成.
∴(![]() +
+![]() )×2+
)×2+![]() x=1,
x=1,
解得:x=10.
答:余下的工程由乙队单独施工,还要10天完成.


科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
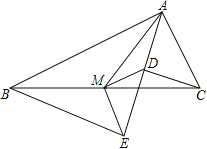
【题目】如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
(1)若AB=8,AC=4,求DE的长;
(2)求证:AB-AC=2DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),将两块直角三角尺的直角顶点C叠放在一起.
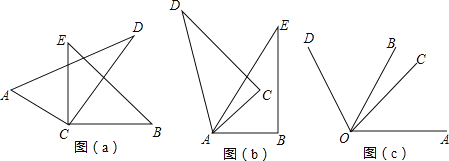
(1)若∠DCE=35°,∠ACB= ;若∠ACB=140°,则∠DCE= ;并猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
(2)如图(b),若是两个同样的三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小有何关系,请说明理由;
(3)已知∠AOB=α,∠COD=β(都是锐角),如图(c),若把它们的顶点O重合在一起,请直接写出∠AOD与∠BOC的大小相等的关系(用含有α,β的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
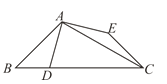
【题目】如图,△ABC中,∠ABC=45°,∠BCA=30°,点D在BC上,点E在△ABC外,且AD=AE=CE,AD⊥AE,则![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
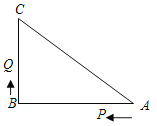
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知轮船A在灯塔P的北偏东30°的方向上,轮船B在灯塔P的南偏东70°的方向上.
(1)求从灯塔P看两轮船的视角(即∠APB)的度数?
(2)轮船C在∠APB的角平分线上,则轮船C在灯塔P的什么方位?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
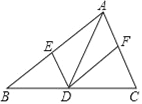
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系xOy中,一次函数y=kx+b的图象l1分别与x轴,y轴交于A(15,0),B两点,正比例函数y=![]() x的图象l2与l1交于点C(m,3).
x的图象l2与l1交于点C(m,3).
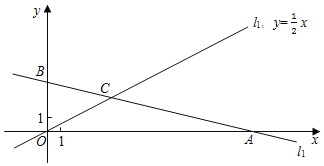
(1)求m的值及l1所对应的一次函数表达式;
(2)根据图象,请直接写出在第一象限内,当一次函数y=kx+b的值大于正比例函数y=![]() x的值时,自变量x的取值范围.
x的值时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com