
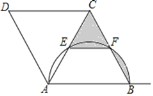
【题目】如图,在菱形ABCD中,以AB为直径画弧分别交BC于点F,交对角线AC于点E,若AB=4,F为BC的中点,则图中阴影部分的面积为 ________;
【答案】![]()
【解析】
如图,取AB的中点O,连接AF,OFAF,OF,BE.证明△ABC是等边三角形与△CEF△BOF,把问题转化为S阴=S扇形OBF,由此即可解决问题.
解:如图,取AB的中点O,连接AF,OF,BE.

∵AB是直径,
∴∠AFB=90°,
∴AF⊥BF,
∵F为BC的中点
∵四边形ABCD是菱形,
∴AB=BC
∴BF=![]()
∴∠BAF=30°,∠B =60°
∴∠BAD=120°
∴∠BAC=60°
∴△ABC是等边三角形,
∴∠ACB=60°
∵AB是直径,
∴∠AEB=90°,
∴AE=![]()
∴E为AC的中点
∴AE=EC=AO=OB,
∴△CEF和△BOF是等边三角形
∴△CEF△BOF
∴S阴=S扇形OBF=![]() ,
,
故答案为:![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
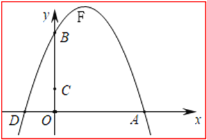
【题目】抛物线![]() 与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,
与y轴交于B,与x轴交于点D、A,点A在点D的右边,顶点为F,![]()
(1)直接写出点B、A、F的坐标;
(2)设Q在该抛物线上,且![]() ,求点Q的坐标;
,求点Q的坐标;
(3)对大于1常数m,在x轴上是否存在点M,使得![]() ?若存在,求出点M坐标;若不存在,说明理由?
?若存在,求出点M坐标;若不存在,说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
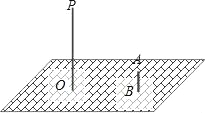
【题目】如图,晚上,小亮在广场上乘凉.图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
(1)请你在图中画出小亮在照明灯(P)照射下的影子;
(2)如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正六面体骰子的六个面分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,如图2,正方形
,如图2,正方形![]() 的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈
的顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子朝上的那面上的数字是几,就沿正方形的边按顺时针方向连续跳几个边长。如:若从圈![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落在圈
个边长,落在圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从圈
,就从圈![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落得圈
个边长,落得圈![]() ;…设游戏者从圈
;…设游戏者从圈![]() 起跳.
起跳.

(1)小贤随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(2)小南随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出他与小贤落回到圈
,并指出他与小贤落回到圈![]() 的可能性一样吗?
的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京剧脸谱是京剧艺术独特的表现形式,现有三张不透明的卡片,其中两张卡片的正面图案为“红脸”,另外一张卡片的正面图案为“黑脸”,卡片除正面图案不同外,其余均相同,将这三张卡片背面向上洗匀,从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图或列表的方法,求抽出的两张卡片上的图案都是“红脸”的概率(图案为“红脸”的两张卡片分别记为![]() 、
、![]() ,图案为“黑脸”的卡片记为
,图案为“黑脸”的卡片记为![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店在服装销售中发现:进货价每件60元,销售价每件100元的某服装每天可售出20件,为了迎接新春佳节,服装店决定采取适当的促销措施,扩大销售量,增加盈利.经调查发现:如果每件服装降价1元,那么每天就可多售出2件.
(1)如果服装店想每天销售这种服装盈利1050元,同时又要使顾客得到更多的实惠,那么每件服装应降价多少元?
(2)每件服装降价多少元时,服装店每天可获得最大利润?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,∠A=90°,AC=4,
中,∠A=90°,AC=4,![]() ,将
,将![]() 沿着斜边BC翻折,点A落在点
沿着斜边BC翻折,点A落在点![]() 处,点D、E分别为边AC、BC的中点,联结DE并延长交
处,点D、E分别为边AC、BC的中点,联结DE并延长交![]() 所在直线于点F,联结
所在直线于点F,联结![]() ,如果
,如果![]() 为直角三角形时,那么
为直角三角形时,那么![]() ____________
____________
查看答案和解析>>
科目:初中数学 来源: 题型:
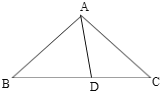
【题目】如图,在等腰△ABC中,AB=AC=4,BC=6点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com