
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB=5£¬AC=9£¬S”÷ABC=![]() £¬¶ÆµćP“ÓAµć³ö·¢£¬ŃŲÉäĻßAB·½ĻņŅŌĆæĆė5øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£¬¶ÆµćQ“ÓCµć³ö·¢£¬ŅŌĻąĶ¬µÄĖŁ¶ČŌŚĻ߶ĪACÉĻÓÉCĻņAŌĖ¶Æ£¬µ±QµćŌĖ¶Æµ½AµćŹ±£¬P”¢QĮ½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£¬ŅŌPQĪŖ±ß×÷Õż·½ŠĪPQEF£ØP”¢Q”¢E”¢F°“ÄꏱÕėÅÅŠņ£©£¬ŅŌCQĪŖ±ßŌŚACÉĻ·½×÷Õż·½ŠĪQCGH£®
£¬¶ÆµćP“ÓAµć³ö·¢£¬ŃŲÉäĻßAB·½ĻņŅŌĆæĆė5øöµ„Ī»µÄĖŁ¶ČŌĖ¶Æ£¬¶ÆµćQ“ÓCµć³ö·¢£¬ŅŌĻąĶ¬µÄĖŁ¶ČŌŚĻ߶ĪACÉĻÓÉCĻņAŌĖ¶Æ£¬µ±QµćŌĖ¶Æµ½AµćŹ±£¬P”¢QĮ½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£¬ŅŌPQĪŖ±ß×÷Õż·½ŠĪPQEF£ØP”¢Q”¢E”¢F°“ÄꏱÕėÅÅŠņ£©£¬ŅŌCQĪŖ±ßŌŚACÉĻ·½×÷Õż·½ŠĪQCGH£®
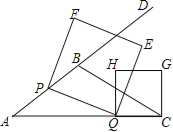
£Ø1£©ĒótanAµÄÖµ£»
£Ø2£©ÉčµćPŌĖ¶ÆŹ±¼äĪŖt£¬Õż·½ŠĪPQEFµÄĆ껿ĪŖS£¬ĒėĢ½¾æSŹĒ·ń“ęŌŚ×īŠ”Öµ£æČō“ęŌŚ£¬Ēó³öÕāøö×īŠ”Öµ£¬Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©µ±tĪŖŗĪÖµŹ±£¬Õż·½ŠĪPQEFµÄijøö¶„µć£ØQµć³żĶā£©ĀäŌŚÕż·½ŠĪQCGHµÄ±ßÉĻ£¬ĒėÖ±½ÓŠ“³ötµÄÖµ£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©“ęŌŚ£®S×īŠ”Öµ=
£»£Ø2£©“ęŌŚ£®S×īŠ”Öµ=![]() £»£Ø3£©t1=
£»£Ø3£©t1=![]() £»t2=
£»t2=![]() £»t3=1£¬t4=
£»t3=1£¬t4=![]() £®
£®
”¾½āĪö”æ
ŹŌĢā£Ø1£©ČēĶ¼1£¬¹żµćB×÷BM”ĶACÓŚµćM£¬ĄūÓĆĆ껿·ØĒóµĆBMµÄ³¤¶Č£¬ĄūÓĆ¹“¹É¶ØĄķµĆµ½AMµÄ³¤¶Č£¬×īŗóÓÉČń½ĒČż½ĒŗÆŹżµÄ¶ØŅå½ųŠŠ½ā“š£»
£Ø2£©ČēĶ¼2£¬¹żµćP×÷PN”ĶACÓŚµćN£®ĄūÓĆ£Ø1£©ÖŠµÄ½įĀŪŗĶ¹“¹É¶ØĄķµĆµ½PN2+NQ2=PQ2£¬ĖłŅŌÓÉÕż·½ŠĪµÄĆ껿¹«Ź½µĆµ½S¹ŲÓŚtµÄ¶ž“ĪŗÆŹż£¬ĄūÓƶž“ĪŗÆŹżµÄ¶„µć×ų±ź¹«Ź½ŗĶ¶ž“ĪŗÆŹżĶ¼ĻóµÄŠŌÖŹĄ“ĒóĘä×īÖµ£»
£Ø3£©ŠčŅŖ·ÖĄąĢÖĀŪ£ŗµ±µćEŌŚ±ßHGÉĻ”¢µćFŌŚ±ßHGÉĻ”¢µćP±ßQH£Ø»ņµćEŌŚQCÉĻ£©”¢µćF±ßCÉĻŹ±Ļą¶ŌÓ¦µÄtµÄÖµ£®
ŹŌĢā½āĪö£ŗ½ā£ŗ£Ø1£©ČēĶ¼1£¬¹żµćB×÷BM”ĶACÓŚµćM£¬
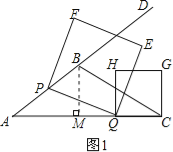
”ßAC=9£¬S”÷ABC=![]() £¬
£¬
”ą![]() ACBM=
ACBM=![]() £¬¼“
£¬¼“![]() ”Į9BM=
”Į9BM=![]() £¬
£¬
½āµĆBM=3£®
Óɹ“¹É¶ØĄķ£¬µĆ
AM=![]() =
=![]() =4£¬
=4£¬
ŌņtanA=![]() =
=![]() £»
£»
£Ø2£©“ęŌŚ£®
ČēĶ¼2£¬¹żµćP×÷PN”ĶACÓŚµćN£®

ŅĄĢāŅāµĆAP=CQ=5t£®
”ßtanA=![]() £¬
£¬
”ąAN=4t£¬PN=3t£®
”ąQN=AC©AN©CQ=9©9t£®
øł¾Ż¹“¹É¶ØĄķµĆµ½£ŗPN2+NQ2=PQ2£¬
SÕż·½ŠĪPQEF=PQ2=£Ø3t£©2+£Ø9©9t£©2=90t2©162t+81£Ø0£¼t£¼![]() £©£®
£©£®
”ß©![]() =
=![]() =
=![]() ŌŚtµÄȔֵ·¶Ī§Ö®ÄŚ£¬
ŌŚtµÄȔֵ·¶Ī§Ö®ÄŚ£¬
”ąS×īŠ”Öµ=![]() =
=![]() =
=![]() £»
£»
£Ø3£©
¢ŁČēĶ¼3£¬µ±µćEŌŚ±ßHGÉĻŹ±£¬t1=![]() £»
£»
¢ŚČēĶ¼4£¬µ±µćFŌŚ±ßHGÉĻŹ±£¬t2=![]() £»
£»
¢ŪČēĶ¼5£¬µ±µćP±ßQH£Ø»ņµćEŌŚQCÉĻ£©Ź±£¬t3=1
¢ÜČēĶ¼6£¬µ±µćF±ßCÉĻŹ±£¬t4=![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijøßæĘ¼¼¹«Ė¾øł¾ŻŹŠ³”ŠčĒó£¬¼Ę»®Éś²śA£¬BĮ½ÖÖŠĶŗŵÄŅ½ĮĘĘ÷Šµ£®Ęä²æ·ÖŠÅĻ¢ČēĻĀ£ŗ
ŠÅĻ¢Ņ»£ŗĆæĢØAŠĶĘ÷ŠµµÄŹŪ¼ŪĪŖ24ĶņŌŖ£¬ĆæĢØBŠĶĘ÷ŠµµÄŹŪ¼ŪĪŖ30ĶņŌŖ£¬ĆæĢØBŠĶĘ÷ŠµµÄÉś²ś³É±¾±ČAŠĶĘ÷ŠµµÄÉś²ś³É±¾¶ą5ĶņŌŖ£®
ŠÅĻ¢¶ž£ŗČōĻśŹŪ3ĢØAŠĶĘ÷ŠµŗĶ5ĢØBŠĶĘ÷Šµ£¬¹²»ńĄū37ĶņŌŖ£»
øł¾ŻÉĻŹöŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒóĆæĢØAŠĶĘ÷Šµ”¢ĆæĢØBŠĶĘ÷ŠµµÄÉś²ś³É±¾ø÷ŹĒ¶ąÉŁĶņŌŖ£æ
£Ø2£©ČōA£¬BĮ½ÖÖŠĶŗŵÄŅ½ĮĘĘ÷Šµ¹²Éś²ś80ĢØ£¬ĒŅøĆ¹«Ė¾Ėł³ļÉś²śŅ½ĮĘĘ÷Šµ×Ź½š²»ÉŁÓŚ1800ĶņŌŖ£¬µ«²»³¬¹ż1810ĶņŌŖ£¬ĒŅ°ŃĖł³ļ׏½šČ«²æÓĆÓŚÉś²ś“ĖĮ½ÖÖŅ½ĮĘĘ÷Šµ£¬øł¾ŻŹŠ³”µ÷²é£¬ĆæĢØAŠĶŅ½ĮĘĘ÷ŠµµÄŹŪ¼Ū½«»įĢįøßaĶņŌŖ£Øa£¾0£©£¬ĆæĢØBŠĶŅ½ĮĘĘ÷ŠµµÄŹŪ¼Ū²»»įøı䣬øĆ¹«Ė¾Ó¦øĆČēŗĪÉś²śæÉŅŌ»ńµĆ×ī“óĄūČó£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬A”¢B”¢C”¢DĪŖ¾ŲŠĪµÄĖÄøö¶„µć£¬AB=16cm£¬AD=6cm£¬¶ÆµćP”¢Q·Ö±š“ÓµćA”¢CĶ¬Ź±³ö·¢£¬µćPŅŌ3cm/sµÄĖŁ¶ČĻņµćBŅĘ¶Æ£¬Ņ»Ö±µ½“ļBĪŖÖ¹£¬µćQŅŌ2cm/sµÄĖŁ¶ČĻņDŅĘ¶Æ£®
(1)P”¢QĮ½µć“Ó³ö·¢æŖŹ¼µ½¼øĆėŹ±£¬ĖıߊĪAPQDĪŖ³¤·½ŠĪ£æ
(2)P”¢QĮ½µć“Ó³ö·¢æŖŹ¼µ½¼øĆėŹ±£æĖıߊĪPBCQµÄĆ껿ĪŖ33cm2£»
(3)P”¢QĮ½µć“Ó³ö·¢æŖŹ¼µ½¼øĆėŹ±£æµćPŗĶµćQµÄ¾ąĄėŹĒ10cm£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬AB£½AC£¬D”¢E”¢F·Ö±šĪŖAB”¢BC”¢ACµÄÖŠµć£¬ŌņĻĀĮŠ½įĀŪ£ŗ¢Ł”÷ADF”Õ”÷FEC£»¢ŚĖıߊĪADEFĪŖĮāŠĪ£»¢Ū![]() ”£ĘäÖŠÕżČ·µÄ½įĀŪŹĒ____________.£ØĢīŠ“ĖłÓŠÕżČ·½įĀŪµÄŠņŗÅ£©
”£ĘäÖŠÕżČ·µÄ½įĀŪŹĒ____________.£ØĢīŠ“ĖłÓŠÕżČ·½įĀŪµÄŠņŗÅ£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µČ±ßČż½ĒŠĪABCµÄ±ß³¤ŹĒ2£¬MŹĒøßCHĖłŌŚÖ±ĻßÉĻµÄŅ»øö¶Æµć£¬Į¬½ÓMB£¬½«Ļ߶ĪBMČʵćBÄꏱÕėŠż×Ŗ60”ćµĆµ½BN£¬Į¬½ÓMN£¬ŌņŌŚµćMŌĖ¶Æ¹ż³ĢÖŠ£¬Ļ߶ĪMN³¤¶ČµÄ×īŠ”ÖµŹĒ£Ø””””£©

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŹé¼®ŹĒČĖĄą½ų²½µÄ½×ĢŻ£¬ĮŖŗĻ¹ś½ĢæĘĪÄ×éÖÆ°ŃĆæÄźµÄ4ŌĀ23ČÕČ·¶ØĪŖ”°ŹĄ½ē¶ĮŹéČÕ”±£¬Ä³Š£ĪŖĮĖĮĖ½āøĆŠ£Ń§ÉśŅ»øöѧʌŌĶĮæĪĶāŹé¼®µÄĒéæö£¬ŌŚČ«Š£·¶Ī§ÄŚĖ껜¶Ō100Ćūѧɜ½ųŠŠĮĖĪŹ¾ķµ÷²é£¬øł¾Żµ÷²éµÄ½į¹ū£¬»ęÖĘĮĖĶ³¼ĘĶ¼±ķµÄŅ»²æ·Ö£ŗŅ»øöŃ§ĘŚĘ½¾łŅ»ĢģŌĶĮæĪĶāŹé¼®ĖłÓŠŹ±¼äĶ³¼Ę±ķ
Ź±¼ä£Ø·ÖÖÓ£© | 20 | 40 | 60 | 80 | 100 | 120 |
ČĖŹż | 43 | 31 | 15 | 5 | 4 | 2 |
ĒėÄćøł¾ŻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
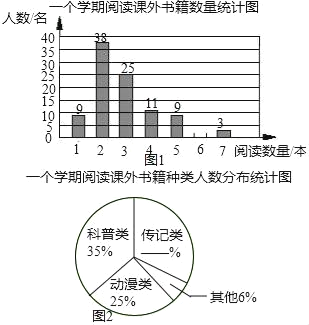
£Ø1£©²¹Č«Ķ¼1”¢Ķ¼2£»
£Ø2£©Õā100ĆūѧɜŅ»øöŃ§ĘŚĘ½¾łĆæČĖŌĶĮæĪĶāŹé¼®¶ąÉŁ±¾£æČōøĆŠ£¹²ÓŠ1200Ćūѧɜ£¬ĒėÄć¹Ą¼ĘÕāøöѧŠ£Ń§ÉśŅ»øöѧʌŌĶĮæĪĶāŹé¼®¹²¶ąÉŁ±¾£æ
£Ø3£©øł¾ŻĶ³¼Ę±ķ£¬ĒóŅ»øöŃ§ĘŚĘ½¾łŅ»ĢģŌĶĮæĪĶāŹé¼®ĖłÓĆŹ±¼äµÄÖŚŹżŗĶÖŠĪ»Źż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼,µćAŹĒŅŌBCĪŖÖ±¾¶µÄ°ėŌ²µÄÖŠµć£¬Į¬½ÓAB£¬µćDŹĒÖ±¾¶BCÉĻŅ»µć£¬Į¬½ÓAD£¬·Ö±š¹żµćB”¢µćCĻņAD×÷“¹Ļߣ¬“¹×ćĪŖEŗĶF£¬ĘäÖŠ£¬EF=2£¬CF=6£¬BE=8£¬ŌņABµÄ³¤ŹĒ£Ø £©
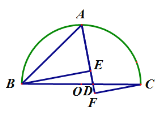
A.4B.6C.8D.10
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾ÅÄź¼¶ŹżŃ§ŠĖȤŠ”×é¾¹żŹŠ³”µ÷²é£¬µĆµ½Ä³ÖÖŌĖ¶Æ·žĆæŌĀµÄĻśĮæŹĒŹŪ¼ŪµÄŅ»“ĪŗÆŹż£¬ĒŅĻą¹ŲŠÅĻ¢ČēĻĀ±ķ£ŗ
ŹŪ¼Ū£ØŌŖ/¼ž£© | 100 | 110 | 120 | 130 | ” |
ŌĀĻśĮæ£Ø¼ž£© | 200 | 180 | 160 | 140 | ” |
ŅŃÖŖøĆŌĖ¶Æ·žµÄ½ų¼ŪĪŖĆ漞60ŌŖ£¬ÉčŹŪ¼ŪĪŖxŌŖ£®
£Ø1£©ĒėÓĆŗ¬xµÄŹ½×Ó±ķŹ¾£ŗ¢ŁĻśŹŪøĆŌĖ¶Æ·žĆ漞µÄĄūČóŹĒ£Ø”” ””£©ŌŖ£»
£Ø2£©ĒóŌĀĻśĮæyÓėŹŪ¼ŪxµÄŅ»“ĪŗÆŹż¹ŲĻµŹ½£ŗ
£Ø3£©ÉčĻśŹŪøĆŌĖ¶Æ·žµÄŌĀĄūČóĪŖWŌŖ£¬ÄĒĆ“ŹŪ¼ŪĪŖ¶ąÉŁŌŖŹ±£¬µ±ŌĀµÄĄūČó×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬![]() µÄĮ½Ö±½Ē±ß
µÄĮ½Ö±½Ē±ß![]() £¬
£¬![]() ·Ö±šŌŚ
·Ö±šŌŚ![]() ÖįµÄøŗ°ėÖįŗĶ
ÖįµÄøŗ°ėÖįŗĶ![]() ÖįµÄÕż°ėÖįÉĻ£¬
ÖįµÄÕż°ėÖįÉĻ£¬![]() ĪŖ×ų±źŌµć£¬
ĪŖ×ų±źŌµć£¬![]() £¬
£¬![]() Į½µćµÄ×ų±ź·Ö±šĪŖ
Į½µćµÄ×ų±ź·Ö±šĪŖ![]() ”¢
”¢![]() £¬Å×ĪļĻß
£¬Å×ĪļĻß![]() ¾¹żµć
¾¹żµć![]() £¬ĒŅ¶„µćŌŚÖ±Ļß
£¬ĒŅ¶„µćŌŚÖ±Ļß![]() ÉĻ£®
ÉĻ£®
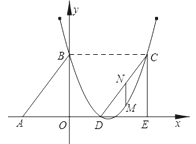
£Ø1£©ĒóÅ×ĪļĻ߶ŌÓ¦µÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©Čō![]() ŹĒÓÉ
ŹĒÓÉ![]() ŃŲ
ŃŲ![]() ÖįĻņÓŅĘ½ŅʵƵ½µÄ£¬µ±ĖıߊĪ
ÖįĻņÓŅĘ½ŅʵƵ½µÄ£¬µ±ĖıߊĪ![]() ŹĒĮāŠĪŹ±£¬ŹŌÅŠ¶Ļµć
ŹĒĮāŠĪŹ±£¬ŹŌÅŠ¶Ļµć![]() ŗĶµć
ŗĶµć![]() ŹĒ·ńŌŚøĆÅ×ĪļĻßÉĻ£¬²¢ĖµĆ÷ĄķÓÉ£»
ŹĒ·ńŌŚøĆÅ×ĪļĻßÉĻ£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Čō![]() µćŹĒ
µćŹĒ![]() ĖłŌŚÖ±ĻßĻĀ·½Å×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬¹żµć
ĖłŌŚÖ±ĻßĻĀ·½Å×ĪļĻßÉĻµÄŅ»øö¶Æµć£¬¹żµć![]() ×÷
×÷![]() Ę½ŠŠÓŚ
Ę½ŠŠÓŚ![]() Öį½»
Öį½»![]() ÓŚ
ÓŚ![]() £®Éčµć
£®Éčµć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬
£¬![]() µÄ³¤¶ČĪŖ
µÄ³¤¶ČĪŖ![]() £®Ēó
£®Ēó![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬Š“³ö×Ō±äĮæ
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£¬Š“³ö×Ō±äĮæ![]() µÄȔֵ·¶Ī§£¬²¢Ēó
µÄȔֵ·¶Ī§£¬²¢Ēó![]() Č”×ī“óÖµŹ±£¬µć
Č”×ī“óÖµŹ±£¬µć![]() µÄ×ų±ź£®
µÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com