
 如图1,点A在第一象限,AB⊥x轴于B点,连结OA,将Rt△AOB折叠,使A点与x轴上的动点A′重合,折痕交AB边于D点,交斜边OA于E点,
如图1,点A在第一象限,AB⊥x轴于B点,连结OA,将Rt△AOB折叠,使A点与x轴上的动点A′重合,折痕交AB边于D点,交斜边OA于E点,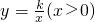 的图象恰好经过D、E两点(如图2),则k=______.
的图象恰好经过D、E两点(如图2),则k=______.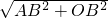 =10,
=10,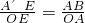 =
= ,
, =
= ,OE=
,OE= ×10=
×10= ,
, =5,
=5,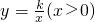 的图象恰好经过D、E两点,
的图象恰好经过D、E两点, b),
b), b,OB=2a,
b,OB=2a, b,
b, b)2=(2a)2+(
b)2=(2a)2+( b)2①,
b)2①, ,b=
,b=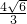 ,
,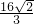 .
.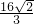 .
.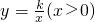 的图象恰好经过D、E两点,可得k=ab,点D的坐标为:(2a,
的图象恰好经过D、E两点,可得k=ab,点D的坐标为:(2a, b),即可得在Rt△OBD中,OD2=OB2+BD2,即(
b),即可得在Rt△OBD中,OD2=OB2+BD2,即( b)2=(2a)2+(
b)2=(2a)2+( b)2①,在Rt△OAB中,OA2=OB2+AB2,即82=(2a)2+(2b)2②,联立求解即可求得答案.
b)2①,在Rt△OAB中,OA2=OB2+AB2,即82=(2a)2+(2b)2②,联立求解即可求得答案.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
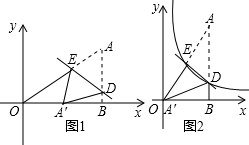 如图1,点A在第一象限,AB⊥x轴于B点,连结OA,将Rt△AOB折叠,使A点与x轴上的动点A′重合,折痕交AB边于D点,交斜边OA于E点,
如图1,点A在第一象限,AB⊥x轴于B点,连结OA,将Rt△AOB折叠,使A点与x轴上的动点A′重合,折痕交AB边于D点,交斜边OA于E点,| k |
| x |
16
| ||
| 3 |
16
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,函数y=
如图,函数y=| 5 |
| x |
| 5 |
| x |
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华市义乌市苏溪中学中考数学模拟试卷(3月份)(解析版) 题型:填空题
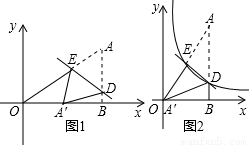 如图1,点A在第一象限,AB⊥x轴于B点,连结OA,将Rt△AOB折叠,使A点与x轴上的动点A′重合,折痕交AB边于D点,交斜边OA于E点,
如图1,点A在第一象限,AB⊥x轴于B点,连结OA,将Rt△AOB折叠,使A点与x轴上的动点A′重合,折痕交AB边于D点,交斜边OA于E点,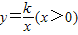 的图象恰好经过D、E两点(如图2),则k= .
的图象恰好经过D、E两点(如图2),则k= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com