
分析 按照有理数的分类填写:
有理数$\left\{\begin{array}{l}整数\left\{\begin{array}{l}正整数\\ 0\\ 负整数\end{array}\right.\\ 分数\left\{\begin{array}{l}正分数\\ 负分数\end{array}\right.\end{array}\right.$.
解答 解:负分数有-1.5,-$\frac{7}{2}$;非负数有2,0,π,|-3.5|;整数有2,0,-1,
故答案为:-1.5,-$\frac{7}{2}$;2,0,π,|-3.5|;2,0,-1.
点评 本题考查了有理数,认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点.注意整数和正数的区别,注意0是整数,但不是正数.


科目:初中数学 来源: 题型:解答题
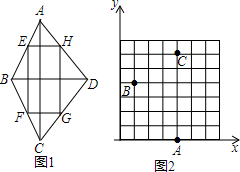

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$和-0.75 | B. | -|-5|和-5 | C. | π和-3.14 | D. | $\frac{1}{3}$和-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
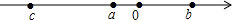 已知a,b,c三个数在数轴上的位置如图所示.
已知a,b,c三个数在数轴上的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com