
【题目】如图,在平面直角坐标系中,直线y=![]() x+6与x、y轴分别交于点A,点B,双曲线的解析式为
x+6与x、y轴分别交于点A,点B,双曲线的解析式为![]()
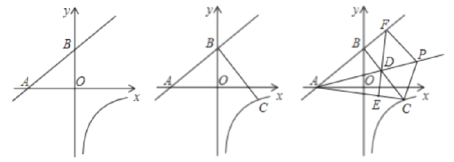
(1)求出线段AB的长
(2)在双曲线第四象限的分支上存在一点C,使得CB⊥AB,且CB=AB,求k的值;
(3)在(1)(2)的条件下,连接AC,点D为BC的中点,过D作AC的垂线BF,交AC于B,交直线AB于F,连AD,若点P为射线AD上的一动点,连接PC、PF,当点P在射线AD上运动时,PF![]() -PC
-PC![]() 的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
【答案】(1)10(2)-12;(3)不变,25
【解析】
(1)首先求出图象与坐标轴交点坐标,进而得出AO,OB的长,即可利用勾股定理求出AB的长;
(2)首先作CD⊥y轴于点D,求出∠BAO=∠CBD再利用△ABO≌△BDC,进而得出C点坐标,即可得出k的值
(3)首先连接FC交AP于M,利用△ABD≌△CBF(SAS),得出∠BAD=∠DCM,进而利用勾股定理求出PF![]() -PC
-PC![]() =DF
=DF![]() -CD
-CD![]() ,求出即可
,求出即可
(1)
由y=![]() x+6与x、y轴分別交于点A,点B,
x+6与x、y轴分別交于点A,点B,
得:x=0时,y=6,y=0时,x=-8
故A(-8,0),B(0,6)
∴AO=8, OB=6
∴AB=![]() =10
=10
(2)作CD⊥y轴于点D,
∵∠ABO+∠BAO=90°,∠CBO+∠ABO=90°,
∴∠BAO=∠CBD
在△ABO和△BDC中,
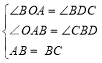
∴△ABO≌△BDC(AAS),
∴CD=OB=6, BD=OA=8
∴OD=BD-OB=8-6=2
∴C(6,-2)
∴k=6×(-2)=-12
(3)连接FC交AP于M
∵AB=BC,∠ABC=90°,
∴∠ACB=45°
∵EF⊥AC
∴∠BDR=∠EDC=45°
∵∠ABC=90°
∴.∠BFD=∠BDF=45°
∴BD=BF
在△ABD和△CBF中
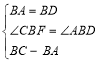
∴△ABD≌△CBF(SAS)
∴∠BAD=∠DCM
∴∠DMC=∠ABD=90°
∴PF![]() -PC
-PC![]() =(FM
=(FM![]() + MP
+ MP![]() )-(CM
)-(CM![]() +MP
+MP![]() )=FM
)=FM![]() -CM
-CM![]() =(DF
=(DF![]() -DM
-DM![]() )-(CD
)-(CD![]() -DM
-DM![]() )=DF
)=DF![]() -CD
-CD![]()
∵D是BC的中点
∴BD=CD=5
.∴BF=5
∴DF=![]() =5
=5![]()
∴PF![]() -PC
-PC![]() =(5
=(5![]() )
) ![]() -5
-5![]() =25
=25


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】为了传承中华优秀传统文化,某校组织了一次八年级350名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 2 | 0.04 |
60≤x<70 | 6 | 0.12 |
70≤x<80 | 9 | b |
80≤x<90 | a | 0.36 |
90≤x≤100 | 15 | 0.30 |
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
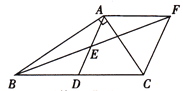
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
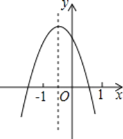
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,分析下列四个结论:①abc<0;②b2-4ac>0;③a+b+c>0;④a-b+c>0.其中正确的结论有( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
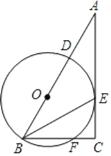
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=12,⊙O的半径为10,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
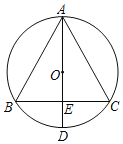
【题目】如图,△ABC内接于⊙O,AD为⊙O的直径,AD与BC相交于点E,且BE=CE.
(1)请判断AD与BC的位置关系,并说明理由;
(2)若BC=6,ED=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入到不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,求抽出的卡片上的数字恰好是偶数的概率;
(2)从中随机抽出2张卡片,求抽出的2张卡片上的数字恰好是相邻两整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间x(单位:分钟)与学习收益量y的关系如图甲所示,用于回顾反思的时间x(单位:分钟)与学习收益量z的关系为z=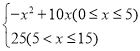 ,且用于回顾反思的时间不超过用于解题的时间.
,且用于回顾反思的时间不超过用于解题的时间.
(1)求王亮解题的学习收益量y与用于解题的时间x之间的函数关系式,并写出自变量x的取值范围;
(2)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?(学习收益总量=解题的学习收益量+回顾反思的学习收益量)
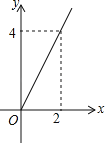
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=![]() 正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
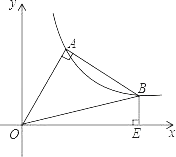
A. 3B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com