
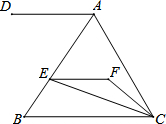
 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=3∠BCF,∠ACF=20°.分析 (1)先根据CE平分∠BCF,设∠BCE=∠ECF=$\frac{1}{2}$∠BCF=x.由∠DAC=3∠BCF可得出∠DAC=6x.根据AD∥EF,AD∥BC,得出EF∥BC,由平行线的性质即可得出x的值,进而得出结论;
(2)根据AD∥BC可知∠DAB=∠B,再由∠BAC=3∠B得出∠DAC=4∠B=120°,故∠B=30°,∠BAC=90°,由此可得出结论;
(3)根据(1)可得出∠BCF的度数,由直角三角形的性质即可得出结论.
解答 (1)解:∵CE平分∠BCF,
∴设∠BCE=∠ECF=$\frac{1}{2}$∠BCF=x.
∵∠DAC=3∠BCF,
∴∠DAC=6x.
∵AD∥EF,AD∥BC,
∴EF∥BC,
∴∠DAC+∠ACB=180°,
∴6x+2x+20=180,
∴x=20°
∴∠BCE=∠FEC=20°;
(2)证明:∵AD∥BC,
∴∠DAB=∠B,
又∵∠BAC=3∠B,
∴∠DAC=4∠B=120°,
∴∠B=30°,
∴∠BAC=90°,
∴AB⊥AC.
(3)解:∵由(1)知∠BCE=20°,
∴∠BCF=40°.
∵当CF⊥AB时,∠B=50°.
∵AD∥BC,
∴∠DAB=50°.
故答案为:50.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.
如图,若直线y=x被双曲线y=$\frac{{k}^{2}}{x}$与双曲线y=$\frac{2{k}^{2}}{x}$在第一象限截得的线段长为2-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.4A | B. | $\sqrt{6}$A | C. | 4.8A | D. | 5$\sqrt{6}$A |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
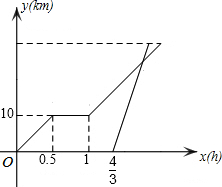 周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1.
在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com