
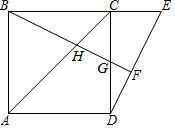
 如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交CD于G.
如图,点E是正方形ABCD的边BC延长线上一点,连结DE,过顶点B作BF⊥DE,垂足为F,BF分别交AC于H,交CD于G.分析 (1)由于BF⊥DE,所以∠GFD=90°,从而可知∠CBG=∠CDE,根据全等三角形的判定即可证明△BCG≌△DCE,从而可知BG=DE;
(2)设CG=1,从而知CG=CE=1,由勾股定理可知:DE=BG=$\sqrt{5}$,由易证△ABH∽△CGH,所以$\frac{BH}{HG}=2$,从而可求出HG的长度,进而求出$\frac{HG}{GF}$的值.
解答 解:(1)∵BF⊥DE,
∴∠GFD=90°,
∵∠BCG=90°,∠BGC=∠DGF,
∴∠CBG=∠CDE,
在△BCG与△DCE中,
$\left\{\begin{array}{l}{∠CBG=∠CDE}\\{BC=CD}\\{∠BCG=∠DCE}\end{array}\right.$
∴△BCG≌△DCE(ASA),
∴BG=DE,
(2)设CG=1,
∵G为CD的中点,
∴GD=CG=1,
由(1)可知:△BCG≌△DCE(ASA),
∴CG=CE=1,
∴由勾股定理可知:DE=BG=$\sqrt{5}$,
∵sin∠CDE=$\frac{CE}{DE}$=$\frac{GF}{GD}$,
∴GF=$\frac{\sqrt{5}}{5}$,
∵AB∥CG,
∴△ABH∽△CGH,
∴$\frac{AB}{CG}=\frac{BH}{GH}$=$\frac{2}{1}$,
∴BH=$\frac{2}{3}$$\sqrt{5}$,GH=$\frac{1}{3}$$\sqrt{5}$,
∴$\frac{HG}{GF}$=$\frac{5}{3}$
点评 本题考查相似三角形的综合问题,涉及相似三角形的判定与性质,全等三角形的判定与性质,勾股定理等知识,综合程度较高,属于中等题型.


科目:初中数学 来源: 题型:选择题
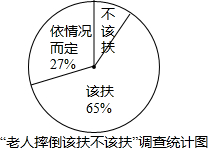 “救死扶伤”是我国的传统美德,某媒体就“老人摔倒该不该扶”进行了调查,将得到的数据经统计分析后绘制成如图所示的扇形统计图,根据统计图判断下列说法,其中错误的一项是( )
“救死扶伤”是我国的传统美德,某媒体就“老人摔倒该不该扶”进行了调查,将得到的数据经统计分析后绘制成如图所示的扇形统计图,根据统计图判断下列说法,其中错误的一项是( )| A. | 认为依情况而定的占27% | |
| B. | 认为该扶的在统计图中所对应的圆心角是234° | |
| C. | 认为不该扶的占8% | |
| D. | 认为该扶的占92% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
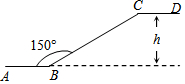 某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )| A. | 4$\sqrt{3}$m | B. | 8m | C. | $\frac{8}{3}$$\sqrt{3}$m | D. | 4m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
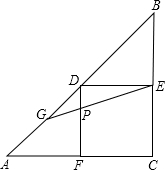 一节课上,数学老师在黑板上给出了这样一道题目:
一节课上,数学老师在黑板上给出了这样一道题目:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com