
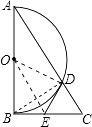
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC与点D,点E为BC的中点,连接DE.
(1)求证:DE是半圆⊙O的切线.
(2)若∠BAC=30°,DE=2,求AD的长.
【答案】
(1)证明:连接OD,OE,BD,
∵AB为圆O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,E为斜边BC的中点,
∴DE=BE,
在△OBE和△ODE中,
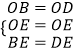 ,
,
∴△OBE≌△ODE(SSS),
∴∠ODE=∠ABC=90°,
则DE为圆O的切线
(2)解:在Rt△ABC中,∠BAC=30°,
∴BC= ![]() AC,
AC,
∵BC=2DE=4,
∴AC=8,
又∵∠C=60°,DE=CE,
∴△DEC为等边三角形,即DC=DE=2,
则AD=AC﹣DC=6
【解析】(1)要证切线可须连半径,再证直线和半径垂直,出现直径时,连直径的端点和圆周上一点构成90°的圆周角,进而利用斜边中线性质可证出;(2)由DE可求出BC,由30°性质可求出AB,再利用三角函数可求出AD.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB与半径为2的⊙O相切于点C,点D,E,F是⊙O上三个点,EF∥AB,若EF=2 ![]() ,则∠EDC的度数为( )
,则∠EDC的度数为( )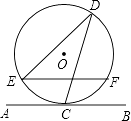
A.60°
B.90°
C.30°
D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________________ ),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小明家和学校所在地的简单地图,已知![]() ,
,![]() ,
,![]() ,点C为OP的中点,回答下列问题:
,点C为OP的中点,回答下列问题:

(1)图中到小明家距离相同的是哪些地方?
(2)由图可知,公园在小明家东偏南30°方向2km处.请用方向与距离描述学校、商场、停车场相对于小明家的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红购买了两次笔记本,购买情况及总费用如下表
购买次数 | 购买各种笔记本的数量 | 购买总费用 | |
甲 | 乙 | ||
第一次 | 1 | 4 | 22 |
第二次 | 2 | 3 | 24 |
![]() 备注:两次购买甲、乙笔记本的单价不变
备注:两次购买甲、乙笔记本的单价不变![]()
![]() 甲、乙笔记本的单价分别是多少元?
甲、乙笔记本的单价分别是多少元?
![]() 小红第三次以相同的价格购买甲、乙两种笔记本共18本,总费用为92元,则小红第三次购买甲、乙笔记本各多少本?
小红第三次以相同的价格购买甲、乙两种笔记本共18本,总费用为92元,则小红第三次购买甲、乙笔记本各多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧 ![]() 的中点,点D是优弧
的中点,点D是优弧 ![]() 上一点,且∠D=30°,下列四个结论:
上一点,且∠D=30°,下列四个结论:
①OA⊥BC;②BC=6 ![]() ;③sin∠AOB=
;③sin∠AOB= ![]() ;④四边形ABOC是菱形.
;④四边形ABOC是菱形.
其中正确结论的序号是( )
A.①③
B.①②③④
C.②③④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,长方形的两边长分别为m+1,m+7;如图②,长方形的两边长分别为m+2,m+4.(其中m为正整数)


(1) 图①中长方形的面积![]() =_______________
=_______________
图②中长方形的面积![]() =_______________
=_______________
比较:![]() ______
______![]() (填“<”、“=”或“>”)
(填“<”、“=”或“>”)
(2) 现有一正方形,其周长与图①中的长方形周长相等,
①求正方形的边长(用含m的代数式表示);
②试说明:该正方形面积![]() 与图①中长方形面积
与图①中长方形面积![]() 的差(即
的差(即![]() -
-![]() )是定值.
)是定值.
(3) 在(1)的条件下,若某个图形的面积介于![]() 、
、![]() 之间(不包括
之间(不包括![]() 、
、![]() )并且面积为整数,这样的整数值有且只有20个,求m的值.
)并且面积为整数,这样的整数值有且只有20个,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com