Question

8．我们知道，三角形的三条中线一定会交于一点，这一点就叫做三角形的重心．请你利用重心的概念完成如下问题：
（1）如图1，若O是△ABC的重心，连结AO并延长交BC于D，证明：$\frac{AO}{AD}$=$\frac{2}{3}$
（2）如图2，若O是△ABC的重心，若AB=5，点G从A出发，在AB边上以每秒一个单位的速度向B运动，运动时间为t秒，连GO，直线GO交直线AC与H点（G、H均不与△ABC的顶点重合）．
①求$\frac{GO}{OH}$（用含有t的式子表示）
②若G、H分别在边AB、AC上，S_{四边形BCHG}，S_△AGH分别表示四边形BCHG和△AGH的面积，直接写出$\frac{{{S_{四边形BCHG}}}}{{{S_{△AGH}}}}$的最大值．

Answer 1

分析 （1）根据题意作出中位线DE，证出△AOC∽△DOE，得出$\frac{AO}{OD}$=$\frac{AC}{DE}$=2，再根据AD=AO+OD，即可得出答案；
（2）过点O作EF∥BC，交AB、AC于E、F，过点F作FM∥AB，交DH于点M，根据给出的条件得出$\frac{AE}{5}$=$\frac{2}{3}$，求出AE和EG，根据△EOG≌△FOM，求出FM=EG=$\frac{10}{3}$-t，根据$\frac{FH}{AH}$=$\frac{FM}{AG}$，求出$\frac{AF}{AH}$=2-$\frac{10}{3t}$，$\frac{EO}{NH}$=$\frac{1}{2}$×（2-$\frac{10}{3t}$），最后根据$\frac{GH}{GO}$=$\frac{3t}{3t-5}$，求出$\frac{OH}{GO}$=$\frac{5}{3t-5}$即可得出$\frac{GO}{OH}$；
过点F作FM∥GH，交GH的延长线于点M，同理可得：FM=GE=t-$\frac{10}{3}$，根据$\frac{FM}{AG}$=$\frac{FH}{AH}$=$\frac{t-\frac{10}{3}}{t}$，求出$\frac{EF}{NH}$=2-$\frac{10}{3t}$，最后根据$\frac{GO}{GH}$=1-$\frac{5}{3t}$即可得出$\frac{GO}{OH}$=$\frac{3}{5}$t-1；
（3）连接DG，设S_△GOD=S，根据（1）得出S_△AOG=2S，S_△AGD=S_△GOD+S_△AGO=3S，设AG=1，BG=x，则S_△BGD=3xS，从而得出S_△ABC=2S_△ABD=（6x+6）S，再根据S_{四边形BCHG}=S_△ABC-S_△AGH，求出$\frac{{{S_{四边形BCHG}}}}{{{S_{△AGH}}}}$的值，过点O作OF∥BC交AC于点F，过点G作GE∥BC交AC于点E，则OF∥GE，求出OF=$\frac{2}{3}$ CD=$\frac{1}{3}$BC，再根据平行线的性质得出GE=$\frac{BC}{x+1}$和$\frac{OH}{GH-OH}$=$\frac{OF}{GE-OF}$，求出k的值，得出$\frac{{{S_{四边形BCHG}}}}{{{S_{△AGH}}}}$=$\frac{3x-k+2}{k+1}$=-x²+x+1=-（x-$\frac{1}{2}$）²+$\frac{5}{4}$，从而得出$\frac{{{S_{四边形BCHG}}}}{{{S_{△AGH}}}}$的最大值．

解答 解：（1）如图1所示，连接CO并延长，交AB于点E，
∵点O是△ABC的重心，
∴CE是中线，点E是AB的中点．
∴DE是中位线，
∴DE∥AC，且DE=$\frac{1}{2}$AC．
∵DE∥AC，
∴△AOC∽△DOE．
∴$\frac{AO}{OD}$=$\frac{AC}{DE}$=2，
∵AD=AO+OD，
∴$\frac{AO}{AD}$=$\frac{2}{3}$；

（2）①过点O作EF∥BC，交AB、AC于E、F，
过点F作FM∥AB，交GH于点M，
∵AG=t，
∴BG=5-t，
∵$\frac{AE}{AB}$=$\frac{AO}{AD}$=$\frac{2}{3}$，
∴$\frac{AE}{5}$=$\frac{2}{3}$，
∴AE=$\frac{10}{3}$，
∴EG=$\frac{10}{3}$-t，
∵$\frac{EO}{BD}$=$\frac{OF}{CD}$，
∴EO=FO，
在△EOG和△FOM中，
$\left\{\begin{array}{l}{∠EOG=∠FOM}\\{∠EGO=∠FMO}\\{EO=FO}\end{array}\right.$，
∴△EOG≌△FOM（AAS），
∴FM=EG=$\frac{10}{3}$-t，
∵$\frac{FH}{AH}$=$\frac{FM}{AG}$，
∴$\frac{FH}{AH}$=$\frac{\frac{10}{3}-t}{t}$，
∴1-$\frac{FH}{AH}$=1-$\frac{\frac{10}{3}-t}{t}$，
∴$\frac{AF}{AH}$=2-$\frac{10}{3t}$，
∴$\frac{EF}{MN}$=$\frac{AF}{AH}$=2-$\frac{10}{3t}$，
∴$\frac{EO}{NH}$=$\frac{1}{2}$×（2-$\frac{10}{3t}$），
∴$\frac{GO}{GH}$=$\frac{EO}{NH}$=1-$\frac{5}{3t}$=$\frac{3t-5}{3t}$，
∴$\frac{GH}{GO}$=$\frac{3t}{3t-5}$，
∴$\frac{GH}{GO}$-1=$\frac{3t}{3t-5}$-1，
∴$\frac{OH}{GO}$=$\frac{5}{3t-5}$，
∴$\frac{GO}{OH}$=$\frac{3}{5}$t-1；
②如图3：过点F作FM∥GH，交GH的延长线于点M，
同理可得：FM=GE=t-$\frac{10}{3}$，
∵$\frac{FM}{AG}$=$\frac{FH}{AH}$=$\frac{t-\frac{10}{3}}{t}$，
∴$\frac{AF}{AH}$=$\frac{t-\frac{10}{3}}{t}$+1=2-$\frac{10}{3t}$，
∴$\frac{EF}{NH}$=2-$\frac{10}{3t}$，
∴$\frac{EO}{AH}$=$\frac{1}{2}$（2-$\frac{10}{3t}$）=1-$\frac{5}{3t}$，
∴$\frac{GO}{GH}$=1-$\frac{5}{3t}$，
∴$\frac{GO}{OH}$=$\frac{3}{5}$t-1；

（3）如图4，连接DG，
设S_△GOD=S，由（1）知$\frac{AO}{AD}$=$\frac{2}{3}$，即OA=2OD，
∴S_△AOG=2S，S_△AGD=S_△GOD+S_△AGO=3S，
设AG=1，BG=x，则S_△BGD=3xS，
∴S_△ABD=S_△AGD+S_△BGD=3S+3xS=（3x+3）S．
∴S_△ABC=2S_△ABD=（6x+6）S，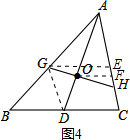
设OH=kOG，由S_△AGO=2S，得S_△AOH=2kS，
∴S_△AGH=S_△AGO+S_△AOH=（2k+2）S．
∴S_{四边形BCHG}=S_△ABC-S_△AGH=（6x+6）S-（2k+2）S=（6x-2k+4）S，
∴$\frac{{{S_{四边形BCHG}}}}{{{S_{△AGH}}}}$=$\frac{（6x-2k+4）S}{（2k+2）S}$=$\frac{3x-k+2}{k+1}$ ①，
过点O作OF∥BC交AC于点F，过点G作GE∥BC交AC于点E，则OF∥GE，
∵OF∥BC，
∴$\frac{OF}{CD}$=$\frac{AO}{AD}$=$\frac{2}{3}$，
∴OF=$\frac{2}{3}$ CD=$\frac{1}{3}$BC，
∵GE∥BC，
∴$\frac{GE}{BC}$=$\frac{AG}{AB}$=$\frac{1}{x+1}$，
∴GE=$\frac{BC}{x+1}$，
∴$\frac{OF}{GE}$=$\frac{\frac{1}{3}BC}{\frac{BC}{x+1}}$=$\frac{x+1}{3}$，
∴$\frac{OF}{GE-OF}$=$\frac{x+1}{3-（x+1）}$=$\frac{x+1}{2-x}$，
∵OF∥GE，
∴$\frac{OH}{GH}$=$\frac{OF}{GE}$，
∴$\frac{OH}{GH-OH}$=$\frac{OF}{GE-OF}$，即$\frac{OH}{OG}$=$\frac{OF}{GE-OF}$=$\frac{x+1}{2-x}$，
∴k=$\frac{x+1}{2-x}$，代入①式得：
$\frac{{{S_{四边形BCHG}}}}{{{S_{△AGH}}}}$=$\frac{3x-k+2}{k+1}$=$\frac{3x-\frac{x+1}{2-x}+2}{\frac{x+1}{2-x}}$=-x²+x+1=-（x-$\frac{1}{2}$）²+$\frac{5}{4}$，
∴当x=$\frac{1}{2}$ 时，$\frac{{{S_{四边形BCHG}}}}{{{S_{△AGH}}}}$有最大值，最大值为$\frac{5}{4}$．

点评 此题考查了相似形的综合，用到的知识点是重心的定义、相似三角形和全等三角形的判定与性质、平行线的性质等知识点，本题难度较大，关键是根据题意画出图形，注意不要漏解．